Примечание
Перейти в конец чтобы скачать полный пример кода или запустить этот пример в браузере через JupyterLite или Binder.
Precision-Recall#
Пример использования метрики Precision-Recall для оценки качества выходных данных классификатора.
Precision-Recall — полезная мера успешности предсказания, когда классы сильно несбалансированы. В информационном поиске precision — это мера доли релевантных элементов среди фактически возвращённых элементов, а recall — мера доли элементов, которые были возвращены, среди всех элементов, которые должны были быть возвращены. «Релевантность» здесь относится к элементам, которые помечены положительно, т.е. true positives и false negatives.
Точность (\(P\)) определяется как количество истинно положительных (\(T_p\)) по количеству истинно положительных плюс количество ложноположительных (\(F_p\)).
Полнота (\(R\)) определяется как количество истинно положительных (\(T_p\)) над числом истинно положительных плюс число ложно отрицательных (\(F_n\)).
Кривая точности-полноты показывает компромисс между точностью и полнотой при различных порогах. Большая площадь под кривой означает как высокую полноту, так и высокую точность. Высокая точность достигается за счет малого количества ложноположительных результатов, а высокая полнота - за счет малого количества ложноотрицательных результатов среди релевантных. Высокие значения обеих метрик показывают, что классификатор возвращает точные результаты (высокая точность), а также возвращает большинство всех релевантных результатов (высокая полнота).
Система с высокой полнотой, но низкой точностью возвращает большинство релевантных элементов, но доля возвращённых результатов, которые неправильно помечены, высока. Система с высокой точностью, но низкой полнотой является противоположностью, возвращая очень мало релевантных элементов, но большинство её предсказанных меток верны при сравнении с фактическими метками. Идеальная система с высокой точностью и высокой полнотой вернёт большинство релевантных элементов, причём большинство результатов будут правильно помечены.
Определение точности (\(\frac{T_p}{T_p + F_p}\)) показывает, что снижение порога классификатора может увеличить знаменатель, увеличивая количество возвращаемых результатов. Если порог был ранее установлен слишком высоко, новые результаты могут быть истинно положительными, что повысит точность. Если предыдущий порог был примерно правильным или слишком низким, дальнейшее снижение порога приведет к ложным срабатываниям, снижая точность.
Полнота определяется как \(\frac{T_p}{T_p+F_n}\), где \(T_p+F_n\) не зависит от порога классификатора. Изменение порога классификатора может изменить только числитель, \(T_p\). Понижение порога классификатора может увеличить полноту, увеличив количество истинно положительных результатов. Также возможно, что понижение порога оставит полноту неизменной, в то время как точность колеблется. Таким образом, точность не обязательно уменьшается с увеличением полноты.
Связь между полнотой и точностью можно наблюдать в ступенчатой области графика - на краях этих ступеней небольшое изменение порога значительно снижает точность, с лишь незначительным увеличением полноты.
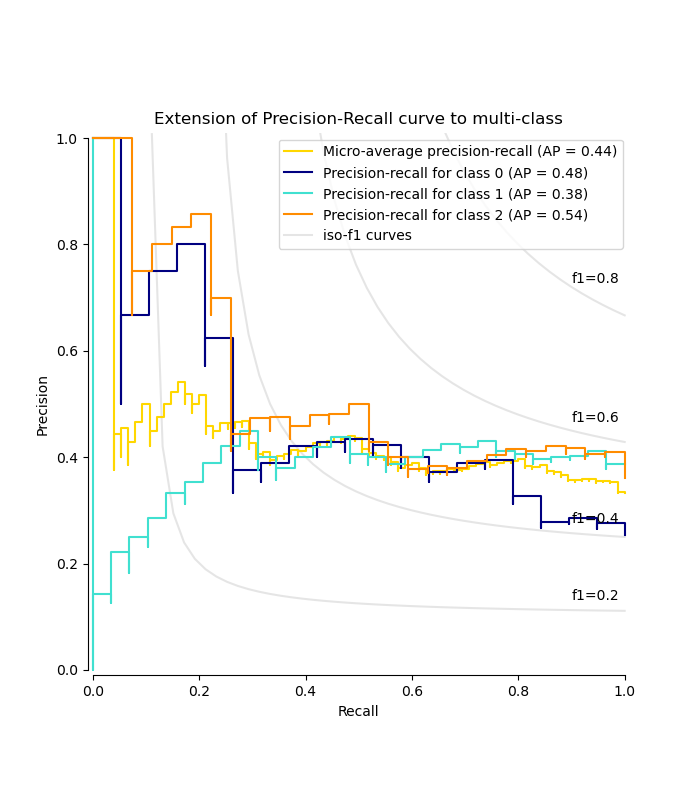
Средняя точность (AP) суммирует такой график как взвешенное среднее достигнутых точностей на каждом пороге, с увеличением полноты от предыдущего порога, используемым в качестве веса:
\(\text{AP} = \sum_n (R_n - R_{n-1}) P_n\)
где \(P_n\) и \(R_n\) являются точностью и полнотой на n-м пороге. Пара \((R_k, P_k)\) называется рабочая точка.
AP и площадь под операционной характеристикой по трапециевидному правилу (sklearn.metrics.auc) являются распространенными способами обобщения кривой
точности-полноты, которые приводят к разным результатам. Подробнее в
Руководство пользователя.
Кривые точности-полноты обычно используются в бинарной классификации для изучения выходных данных классификатора. Чтобы расширить кривую точности-полноты и среднюю точность на многоклассовую или многометочную классификацию, необходимо бинаризировать выход. Можно построить одну кривую для каждой метки, но также можно построить кривую точности-полноты, рассматривая каждый элемент матрицы индикаторов меток как бинарный прогноз (микро-усреднение).
Примечание
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
В настройках бинарной классификации#
Набор данных и модель#
Мы будем использовать классификатор Linear SVC для различения двух типов ирисов.
import numpy as np
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
X, y = load_iris(return_X_y=True)
# Add noisy features
random_state = np.random.RandomState(0)
n_samples, n_features = X.shape
X = np.concatenate([X, random_state.randn(n_samples, 200 * n_features)], axis=1)
# Limit to the two first classes, and split into training and test
X_train, X_test, y_train, y_test = train_test_split(
X[y < 2], y[y < 2], test_size=0.5, random_state=random_state
)
Linear SVC ожидает, что каждый признак будет иметь схожий диапазон значений. Поэтому мы сначала масштабируем данные с помощью
StandardScaler.
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.svm import LinearSVC
classifier = make_pipeline(StandardScaler(), LinearSVC(random_state=random_state))
classifier.fit(X_train, y_train)
Построение кривой Precision-Recall#
Чтобы построить кривую точности-полноты, следует использовать
PrecisionRecallDisplay. Действительно, доступны два
метода в зависимости от того, были ли уже вычислены предсказания
классификатора или нет.
Давайте сначала построим кривую точности-полноты без предсказаний классификатора. Мы используем
from_estimator которая вычисляет прогнозы для нас перед построением кривой.
from sklearn.metrics import PrecisionRecallDisplay
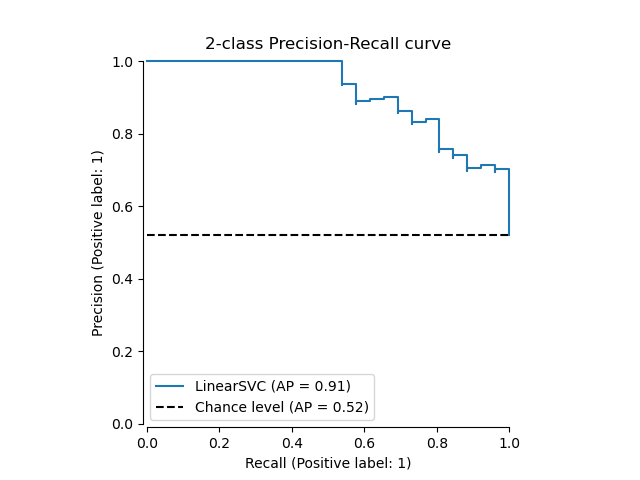
display = PrecisionRecallDisplay.from_estimator(
classifier, X_test, y_test, name="LinearSVC", plot_chance_level=True, despine=True
)
_ = display.ax_.set_title("2-class Precision-Recall curve")
Если у нас уже есть оцененные вероятности или оценки для
нашей модели, то мы можем использовать
from_predictions.
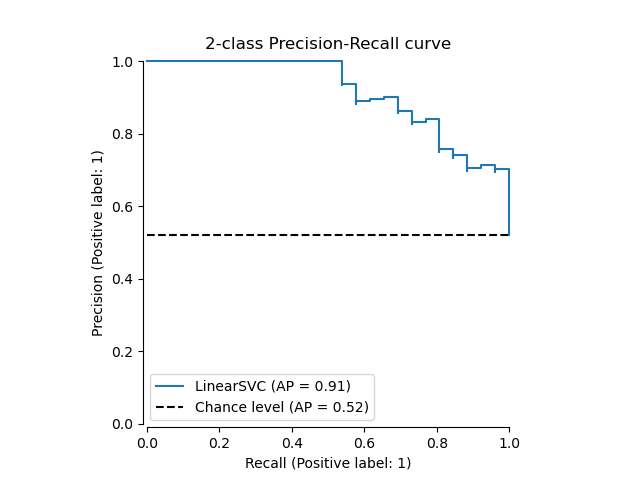
y_score = classifier.decision_function(X_test)
display = PrecisionRecallDisplay.from_predictions(
y_test, y_score, name="LinearSVC", plot_chance_level=True, despine=True
)
_ = display.ax_.set_title("2-class Precision-Recall curve")
В многометочных настройках#
Кривая точности-полноты не поддерживает многометочную настройку. Однако, можно решить, как обрабатывать этот случай. Мы покажем такой пример ниже.
Создание многометочных данных, обучение и предсказание#
Мы создаем многометочный набор данных, чтобы проиллюстрировать точность-полноту в многометочных настройках.
from sklearn.preprocessing import label_binarize
# Use label_binarize to be multi-label like settings
Y = label_binarize(y, classes=[0, 1, 2])
n_classes = Y.shape[1]
# Split into training and test
X_train, X_test, Y_train, Y_test = train_test_split(
X, Y, test_size=0.5, random_state=random_state
)
Мы используем OneVsRestClassifier для многометочного прогнозирования.
from sklearn.multiclass import OneVsRestClassifier
classifier = OneVsRestClassifier(
make_pipeline(StandardScaler(), LinearSVC(random_state=random_state))
)
classifier.fit(X_train, Y_train)
y_score = classifier.decision_function(X_test)
Средняя точность в многометочных настройках#
from sklearn.metrics import average_precision_score, precision_recall_curve
# For each class
precision = dict()
recall = dict()
average_precision = dict()
for i in range(n_classes):
precision[i], recall[i], _ = precision_recall_curve(Y_test[:, i], y_score[:, i])
average_precision[i] = average_precision_score(Y_test[:, i], y_score[:, i])
# A "micro-average": quantifying score on all classes jointly
precision["micro"], recall["micro"], _ = precision_recall_curve(
Y_test.ravel(), y_score.ravel()
)
average_precision["micro"] = average_precision_score(Y_test, y_score, average="micro")
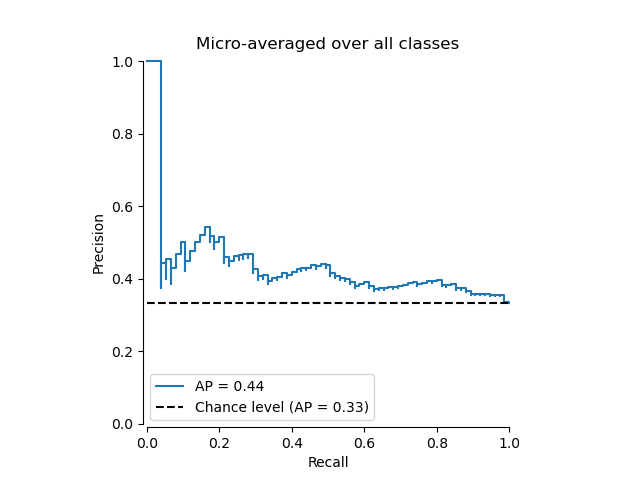
Построение микроусредненной кривой точности-полноты#
from collections import Counter
display = PrecisionRecallDisplay(
recall=recall["micro"],
precision=precision["micro"],
average_precision=average_precision["micro"],
prevalence_pos_label=Counter(Y_test.ravel())[1] / Y_test.size,
)
display.plot(plot_chance_level=True, despine=True)
_ = display.ax_.set_title("Micro-averaged over all classes")
Построение кривой Precision-Recall для каждого класса и кривых iso-f1#
from itertools import cycle
import matplotlib.pyplot as plt
# setup plot details
colors = cycle(["navy", "turquoise", "darkorange", "cornflowerblue", "teal"])
_, ax = plt.subplots(figsize=(7, 8))
f_scores = np.linspace(0.2, 0.8, num=4)
lines, labels = [], []
for f_score in f_scores:
x = np.linspace(0.01, 1)
y = f_score * x / (2 * x - f_score)
(l,) = plt.plot(x[y >= 0], y[y >= 0], color="gray", alpha=0.2)
plt.annotate("f1={0:0.1f}".format(f_score), xy=(0.9, y[45] + 0.02))
display = PrecisionRecallDisplay(
recall=recall["micro"],
precision=precision["micro"],
average_precision=average_precision["micro"],
)
display.plot(ax=ax, name="Micro-average precision-recall", color="gold")
for i, color in zip(range(n_classes), colors):
display = PrecisionRecallDisplay(
recall=recall[i],
precision=precision[i],
average_precision=average_precision[i],
)
display.plot(
ax=ax, name=f"Precision-recall for class {i}", color=color, despine=True
)
# add the legend for the iso-f1 curves
handles, labels = display.ax_.get_legend_handles_labels()
handles.extend([l])
labels.extend(["iso-f1 curves"])
# set the legend and the axes
ax.legend(handles=handles, labels=labels, loc="best")
ax.set_title("Extension of Precision-Recall curve to multi-class")
plt.show()
Общее время выполнения скрипта: (0 минут 0.320 секунд)
Связанные примеры

Пользовательская стратегия повторного обучения для поиска по сетке с кросс-валидацией
Последующая настройка порога принятия решений для обучения с учетом стоимости