spectral_clustering#
- sklearn.cluster.spectral_clustering(affinity, *, n_clusters=8, n_components=None, eigen_solver=None, random_state=None, n_init=10, eigen_tol='auto', assign_labels='kmeans', verbose=False)[источник]#
Применить кластеризацию к проекции нормализованного лапласиана.
На практике спектральная кластеризация очень полезна, когда структура отдельных кластеров сильно невыпуклая или, в более общем смысле, когда мера центра и разброса кластера не является подходящим описанием всего кластера. Например, когда кластеры представляют собой вложенные круги на 2D плоскости.
Если сходство является матрицей смежности графа, этот метод может быть использован для нахождения нормализованных разрезов графа [1], [2].
Подробнее в Руководство пользователя.
- Параметры:
- affinity{array-like, sparse matrix} формы (n_samples, n_samples)
Матрица сходства, описывающая взаимосвязь образцов для встраивания. Должна быть симметричной.
- Возможные примеры:
матрица смежности графа,
тепловое ядро матрицы попарных расстояний образцов,
симметричная матрица связности k-ближайших соседей образцов.
- n_clustersint, default=None
Количество кластеров для извлечения.
- n_componentsint, по умолчанию=n_clusters
Количество собственных векторов для использования в спектральном вложении.
- eigen_solver{None, 'arpack', 'lobpcg' или 'amg'}
Метод разложения по собственным значениям. Если None, то
'arpack'используется. Смотрите [4] для получения дополнительных сведений о'lobpcg'. Решатель собственных значений'amg'запуски'lobpcg'с опциональным предобуславливанием Алгебраического Многосеточного метода и требует установки pyamg. Может работать быстрее на очень больших разреженных задачах [6] и [7].- random_stateint, экземпляр RandomState, по умолчанию=None
Псевдослучайный генератор чисел, используемый для инициализации разложения собственных векторов lobpcg, когда
eigen_solver == 'amg', и для инициализации K-Means. Используйте целое число, чтобы результаты были детерминированными между вызовами (см. Глоссарий).Примечание
При использовании
eigen_solver == 'amg', необходимо также зафиксировать глобальное начальное значение numpy с помощьюnp.random.seed(int)для получения детерминированных результатов. См. pyamg/pyamg#139 для дополнительной информации.- n_initint, по умолчанию=10
Количество запусков алгоритма k-средних с разными начальными центрами. Конечные результаты будут лучшим выводом из n_init последовательных запусков с точки зрения инерции. Используется только если
assign_labels='kmeans'.- eigen_tolfloat, по умолчанию="auto"
Критерий остановки для собственного разложения матрицы Лапласа. Если
eigen_tol="auto"тогда переданный допуск будет зависеть отeigen_solver:Если
eigen_solver="arpack", затемeigen_tol=0.0;Если
eigen_solver="lobpcg"илиeigen_solver="amg", затемeigen_tol=Noneкоторый настраивает базовыйlobpcgрешатель для автоматического разрешения значения согласно их эвристикам. Смотрите,scipy.sparse.linalg.lobpcgподробности.
Обратите внимание, что при использовании
eigen_solver="lobpcg"илиeigen_solver="amg"значенияtol<1e-5может привести к проблемам сходимости и должен быть избегаем.Добавлено в версии 1.2: Добавлена опция 'auto'.
- assign_labels{‘kmeans’, ‘discretize’, ‘cluster_qr’}, по умолчанию=’kmeans’
Стратегия назначения меток в пространстве вложения. Существует три способа назначения меток после лапласианского вложения. Можно применить k-means, что является популярным выбором. Но он также может быть чувствителен к инициализации. Дискретизация - другой подход, который менее чувствителен к случайной инициализации [3]. Метод cluster_qr [5] список формы ( Сегментация изображения греческих монет на регионы.
Изменено в версии 1.1: Добавлен новый метод маркировки 'cluster_qr'.
- verbosebool, по умолчанию=False
Режим подробности.
Добавлено в версии 0.24.
- Возвращает:
- меткимассив целых чисел, форма: n_samples
Метки кластеров.
Примечания
Граф должен содержать только одну связную компоненту, иначе результаты имеют мало смысла.
Этот алгоритм решает нормализованный разрез для
k=2: это нормализованная спектральная кластеризация.Ссылки
Примеры
>>> import numpy as np >>> from sklearn.metrics.pairwise import pairwise_kernels >>> from sklearn.cluster import spectral_clustering >>> X = np.array([[1, 1], [2, 1], [1, 0], ... [4, 7], [3, 5], [3, 6]]) >>> affinity = pairwise_kernels(X, metric='rbf') >>> spectral_clustering( ... affinity=affinity, n_clusters=2, assign_labels="discretize", random_state=0 ... ) array([1, 1, 1, 0, 0, 0])
Примеры галереи#

Сегментация изображения греческих монет на регионы
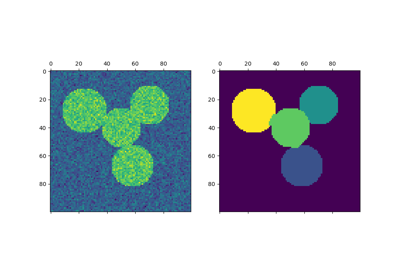
Спектральная кластеризация для сегментации изображений