Примечание
Перейти в конец чтобы скачать полный пример кода или запустить этот пример в браузере через JupyterLite или Binder.
Построение границ классификации с различными ядрами SVM#
Этот пример показывает, как различные ядра в SVC (Support Vector
Classifier) влияют на границы классификации в бинарной, двумерной
задаче классификации.
SVC стремятся найти гиперплоскость, которая эффективно разделяет классы в их обучающих
данных, максимизируя зазор между крайними точками данных каждого класса. Это
достигается путем нахождения наилучшего вектора весов \(w\) которая определяет разделяющую гиперплоскость и минимизирует сумму потерь с шарниром для неправильно классифицированных образцов, измеряемую hinge_loss функцию. По умолчанию регуляризация применяется с параметром C=1, что позволяет определенную степень допуска к ошибочной классификации.
Если данные не являются линейно разделимыми в исходном пространстве признаков, может быть установлено нелинейное ядро
параметр. В зависимости от ядра, процесс включает добавление новых признаков
или преобразование существующих признаков для обогащения и потенциального добавления смысла данным.
Когда ядро отлично от "linear" установлен, SVC применяет ядерный трюк, который
вычисляет сходство между парами точек данных с использованием ядерной функции без
явного преобразования всего набора данных. Ядерный трюк превосходит иначе
необходимое матричное преобразование всего набора данных, рассматривая только отношения
между всеми парами точек данных. Ядерная функция отображает два вектора (каждую пару
наблюдений) в их сходство с использованием их скалярного произведения.
Гиперплоскость может быть затем вычислена с использованием функции ядра, как если бы набор данных был представлен в пространстве более высокой размерности. Использование функции ядра вместо явного матричного преобразования улучшает производительность, так как функция ядра имеет временную сложность \(O({n}^2)\), тогда как матричное преобразование масштабируется в соответствии с конкретным применяемым преобразованием.
В этом примере мы сравниваем наиболее распространенные типы ядер машин опорных векторов:
линейное ядро ("linear"), полиномиальное ядро ("poly"), радиальная базисная функция ядра ("rbf") и сигмоидальное ядро ("sigmoid").
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
Создание набора данных#
Мы создаем двумерный набор данных для классификации с 16 образцами и двумя классами. Мы строим график образцов с цветами, соответствующими их целевым значениям.
import matplotlib.pyplot as plt
import numpy as np
X = np.array(
[
[0.4, -0.7],
[-1.5, -1.0],
[-1.4, -0.9],
[-1.3, -1.2],
[-1.1, -0.2],
[-1.2, -0.4],
[-0.5, 1.2],
[-1.5, 2.1],
[1.0, 1.0],
[1.3, 0.8],
[1.2, 0.5],
[0.2, -2.0],
[0.5, -2.4],
[0.2, -2.3],
[0.0, -2.7],
[1.3, 2.1],
]
)
y = np.array([0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1])
# Plotting settings
fig, ax = plt.subplots(figsize=(4, 3))
x_min, x_max, y_min, y_max = -3, 3, -3, 3
ax.set(xlim=(x_min, x_max), ylim=(y_min, y_max))
# Plot samples by color and add legend
scatter = ax.scatter(X[:, 0], X[:, 1], s=150, c=y, label=y, edgecolors="k")
ax.legend(*scatter.legend_elements(), loc="upper right", title="Classes")
ax.set_title("Samples in two-dimensional feature space")
plt.show()
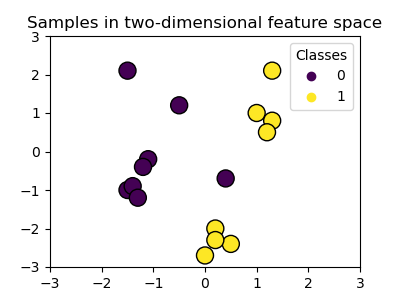
Мы видим, что образцы не могут быть четко разделены прямой линией.
Обучение модели SVC и построение границ решений#
Мы определяем функцию, которая обучает SVC классификатор,
позволяющий kernel параметр в качестве ввода, а затем отображает границы решений, изученные моделью, с использованием
DecisionBoundaryDisplay.
Обратите внимание, что для простоты C параметр установлен в значение по
умолчанию (C=1) в этом примере и gamma параметр установлен в
gamma=2 для всех ядер, хотя он автоматически игнорируется для линейного ядра. В реальной задаче классификации, где важна производительность, настройка параметров (с использованием GridSearchCV например) настоятельно рекомендуется для захвата различных структур в данных.
Установка response_method="predict" в
DecisionBoundaryDisplay окрашивает области на основе
их предсказанного класса. Использование response_method="decision_function" позволяет
нам также построить границу решений и отступы с обеих сторон от нее.
Наконец, опорные векторы, используемые во время обучения (которые всегда лежат на
отступах), идентифицируются с помощью support_vectors_ атрибут
обученных SVC, также отображается.
from sklearn import svm
from sklearn.inspection import DecisionBoundaryDisplay
def plot_training_data_with_decision_boundary(
kernel, ax=None, long_title=True, support_vectors=True
):
# Train the SVC
clf = svm.SVC(kernel=kernel, gamma=2).fit(X, y)
# Settings for plotting
if ax is None:
_, ax = plt.subplots(figsize=(4, 3))
x_min, x_max, y_min, y_max = -3, 3, -3, 3
ax.set(xlim=(x_min, x_max), ylim=(y_min, y_max))
# Plot decision boundary and margins
common_params = {"estimator": clf, "X": X, "ax": ax}
DecisionBoundaryDisplay.from_estimator(
**common_params,
response_method="predict",
plot_method="pcolormesh",
alpha=0.3,
)
DecisionBoundaryDisplay.from_estimator(
**common_params,
response_method="decision_function",
plot_method="contour",
levels=[-1, 0, 1],
colors=["k", "k", "k"],
linestyles=["--", "-", "--"],
)
if support_vectors:
# Plot bigger circles around samples that serve as support vectors
ax.scatter(
clf.support_vectors_[:, 0],
clf.support_vectors_[:, 1],
s=150,
facecolors="none",
edgecolors="k",
)
# Plot samples by color and add legend
ax.scatter(X[:, 0], X[:, 1], c=y, s=30, edgecolors="k")
ax.legend(*scatter.legend_elements(), loc="upper right", title="Classes")
if long_title:
ax.set_title(f" Decision boundaries of {kernel} kernel in SVC")
else:
ax.set_title(kernel)
if ax is None:
plt.show()
Линейное ядро#
Линейное ядро — это скалярное произведение входных выборок:
Затем он применяется к любой комбинации двух точек данных (выборок) в наборе данных. Скалярное произведение двух точек определяет
cosine_similarity между обеими точками.
Чем выше значение, тем более похожи точки.
plot_training_data_with_decision_boundary("linear")
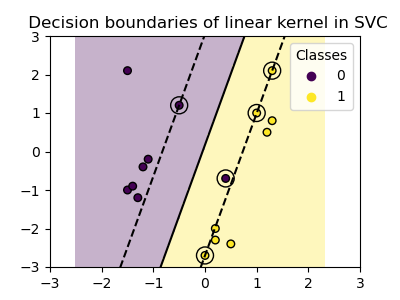
Обучение SVC на линейном ядре приводит к
непреобразованному пространству признаков, где гиперплоскость и поля
являются прямыми линиями. Из-за недостаточной выразительности линейного ядра,
обученные классы не идеально отражают обучающие данные.
Полиномиальное ядро#
Полиномиальное ядро меняет понятие сходства. Функция ядра определяется как:
где \({d}\) это степень (degree) полинома, \({\gamma}\)
(gamma) контролирует влияние каждого отдельного обучающего образца на
границу решения и \({r}\) это член смещения (coef0), который сдвигает
данные вверх или вниз. Здесь мы используем значение по умолчанию для степени
полинома в ядерной функции (degree=3). Когда coef0=0 (по умолчанию), данные только преобразуются, но дополнительное измерение не добавляется. Использование полиномиального ядра эквивалентно созданию
PolynomialFeatures и затем обучение
SVC с линейным ядром на преобразованных данных, хотя этот альтернативный подход был бы вычислительно затратным для большинства наборов данных.
plot_training_data_with_decision_boundary("poly")
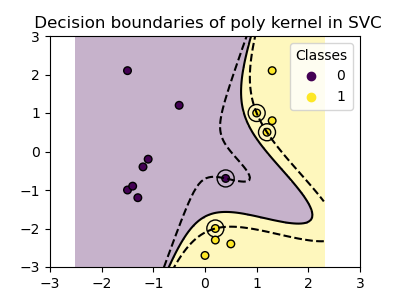
Полиномиальное ядро с gamma=2 хорошо адаптируется к обучающим данным, вызывая изгиб границ по обе стороны гиперплоскости соответственно.
Ядро RBF#
Радиально-базисная функция (RBF), также известная как гауссово ядро, является ядром по умолчанию для метода опорных векторов в scikit-learn. Она измеряет сходство между двумя точками данных в бесконечных размерностях, а затем подходит к классификации по большинству голосов. Функция ядра определяется как:
где \({\gamma}\) (gamma) контролирует влияние каждого отдельного обучающего образца на разделяющую границу.
Чем больше евклидово расстояние между двумя точками \(\|\mathbf{x}_1 - \mathbf{x}_2\|^2\) чем ближе функция ядра к нулю. Это означает, что две удалённые точки с большей вероятностью будут различаться.
plot_training_data_with_decision_boundary("rbf")
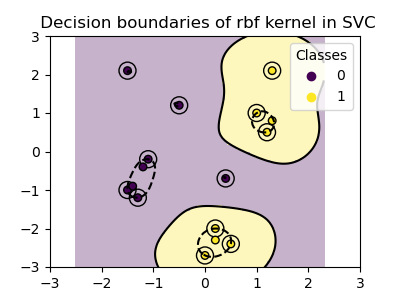
На графике видно, как границы решений стремятся сжиматься вокруг точек данных, которые находятся близко друг к другу.
Сигмоидное ядро#
Сигмоидная функция ядра определяется как:
где коэффициент ядра \({\gamma}\) (gamma) контролирует влияние каждого отдельного обучающего образца на границу решения и \({r}\) является
членом смещения (coef0), который сдвигает данные вверх или вниз.
В сигмоидальном ядре сходство между двумя точками данных вычисляется с использованием гиперболического тангенса (\(\tanh\)). Функция ядра масштабирует и, возможно, смещает скалярное произведение двух точек (\(\mathbf{x}_1\) и \(\mathbf{x}_2\)).
plot_training_data_with_decision_boundary("sigmoid")
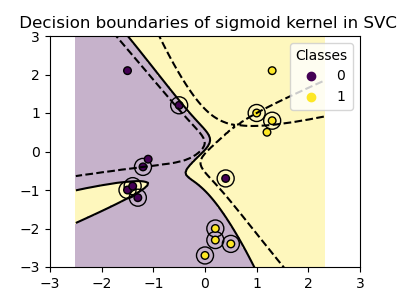
Мы видим, что границы решений, полученные с сигмоидальным ядром, выглядят изогнутыми и неровными. Граница решений пытается разделить классы, подгоняя сигмоидальную кривую, что приводит к сложной границе, которая может плохо обобщаться на невидимые данные. Из этого примера становится очевидно, что сигмоидальное ядро имеет очень специфические случаи применения при работе с данными, которые демонстрируют сигмоидальную форму. В этом примере тщательная тонкая настройка может найти более обобщаемые границы решений. Из-за своей специфичности сигмоидальное ядро реже используется на практике по сравнению с другими ядрами.
Заключение#
В этом примере мы визуализировали границы решений, обученные на предоставленном наборе данных. Графики служат интуитивной демонстрацией того, как разные ядра используют обучающие данные для определения границ классификации.
Гиперплоскости и отступы, хотя вычисляются косвенно, можно представить как плоскости в преобразованном пространстве признаков. Однако на графиках они представлены относительно исходного пространства признаков, что приводит к криволинейным границам решений для полиномиального, RBF и сигмоидного ядер.
Обратите внимание, что графики не оценивают точность или качество отдельных ядер. Они предназначены для визуального понимания того, как разные ядра используют обучающие данные.
Для всесторонней оценки, тонкой настройки SVC
параметры с использованием таких методов, как
GridSearchCV рекомендуется для захвата
основных структур в данных.
Набор данных XOR#
Классический пример набора данных, который не является линейно разделимым, — это паттерн XOR. Здесь мы демонстрируем, как различные ядра работают на таком наборе данных.
xx, yy = np.meshgrid(np.linspace(-3, 3, 500), np.linspace(-3, 3, 500))
np.random.seed(0)
X = np.random.randn(300, 2)
y = np.logical_xor(X[:, 0] > 0, X[:, 1] > 0)
_, ax = plt.subplots(2, 2, figsize=(8, 8))
args = dict(long_title=False, support_vectors=False)
plot_training_data_with_decision_boundary("linear", ax[0, 0], **args)
plot_training_data_with_decision_boundary("poly", ax[0, 1], **args)
plot_training_data_with_decision_boundary("rbf", ax[1, 0], **args)
plot_training_data_with_decision_boundary("sigmoid", ax[1, 1], **args)
plt.show()
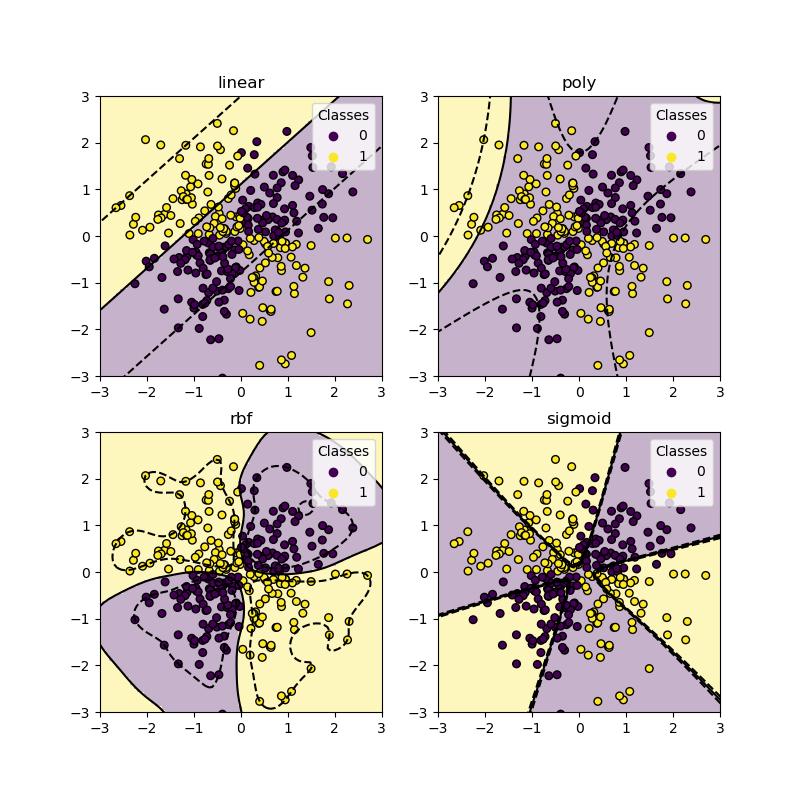
Как видно из графиков выше, только rbf ядро может найти разумную границу решений для приведённого выше набора данных.
Общее время выполнения скрипта: (0 минут 1.188 секунд)
Связанные примеры
Построение различных классификаторов SVM на наборе данных iris
SVM: Разделяющая гиперплоскость с максимальным зазором

SVM: Разделяющая гиперплоскость для несбалансированных классов