Примечание

Перейти в конец чтобы скачать полный пример кода или запустить этот пример в браузере через JupyterLite или Binder.

Влияние сложности модели#

Продемонстрировать, как сложность модели влияет на точность прогнозирования и производительность вычислений.

Мы будем использовать два набора данных:

Набор данных Diabetes для регрессии. Этот набор данных состоит из 10 измерений, взятых у пациентов с диабетом. Задача — предсказать прогрессирование заболевания;
Текстовый набор данных 20 новостных групп для классификации. Этот набор данных состоит из сообщений новостных групп. Задача — предсказать, на какую тему (из 20 тем) написано сообщение.

Мы смоделируем влияние сложности на три различных оценщика:

SGDClassifier (для классификационных данных) который реализует обучение методом стохастического градиентного спуска;
NuSVR (для регрессионных данных), который реализует Nu-метод опорных векторов для регрессии;
GradientBoostingRegressor строит аддитивную модель поэтапно вперед. Обратите внимание, что HistGradientBoostingRegressor намного быстрее, чем GradientBoostingRegressor начиная с промежуточных наборов данных (n_samples >= 10_000), что не относится к этому примеру.

Мы изменяем сложность модели через выбор соответствующих параметров модели в каждой из выбранных моделей. Далее мы измерим влияние на вычислительную производительность (задержку) и предсказательную способность (MSE или потерю Хэмминга).

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

import time

import matplotlib.pyplot as plt
import numpy as np

from sklearn import datasets
from sklearn.ensemble import GradientBoostingRegressor
from sklearn.linear_model import SGDClassifier
from sklearn.metrics import hamming_loss, mean_squared_error
from sklearn.model_selection import train_test_split
from sklearn.svm import NuSVR

# Initialize random generator
np.random.seed(0)

Загрузить данные#

Сначала загружаем оба набора данных.

Примечание

Мы используем fetch_20newsgroups_vectorized для загрузки набора данных 20 новостных групп. Он возвращает готовые к использованию признаки.

Примечание

X набора данных 20 newsgroups является разреженной матрицей, в то время как X набора данных диабета является массивом numpy.

def generate_data(case):
    """Generate regression/classification data."""
    if case == "regression":
        X, y = datasets.load_diabetes(return_X_y=True)
        train_size = 0.8
    elif case == "classification":
        X, y = datasets.fetch_20newsgroups_vectorized(subset="all", return_X_y=True)
        train_size = 0.4  # to make the example run faster

    X_train, X_test, y_train, y_test = train_test_split(
        X, y, train_size=train_size, random_state=0
    )

    data = {"X_train": X_train, "X_test": X_test, "y_train": y_train, "y_test": y_test}
    return data


regression_data = generate_data("regression")
classification_data = generate_data("classification")

Влияние на бенчмарк#

Далее мы можем рассчитать влияние параметров на заданный оценщик. В каждом раунде мы будем устанавливать оценщик с новым значением changing_param и мы будем собирать время предсказания, производительность предсказания и сложности, чтобы увидеть, как эти изменения влияют на оценщик. Мы рассчитаем сложность с помощью complexity_computer переданный как параметр.

def benchmark_influence(conf):
    """
    Benchmark influence of `changing_param` on both MSE and latency.
    """
    prediction_times = []
    prediction_powers = []
    complexities = []
    for param_value in conf["changing_param_values"]:
        conf["tuned_params"][conf["changing_param"]] = param_value
        estimator = conf["estimator"](**conf["tuned_params"])

        print("Benchmarking %s" % estimator)
        estimator.fit(conf["data"]["X_train"], conf["data"]["y_train"])
        conf["postfit_hook"](estimator)
        complexity = conf["complexity_computer"](estimator)
        complexities.append(complexity)
        start_time = time.time()
        for _ in range(conf["n_samples"]):
            y_pred = estimator.predict(conf["data"]["X_test"])
        elapsed_time = (time.time() - start_time) / float(conf["n_samples"])
        prediction_times.append(elapsed_time)
        pred_score = conf["prediction_performance_computer"](
            conf["data"]["y_test"], y_pred
        )
        prediction_powers.append(pred_score)
        print(
            "Complexity: %d | %s: %.4f | Pred. Time: %fs\n"
            % (
                complexity,
                conf["prediction_performance_label"],
                pred_score,
                elapsed_time,
            )
        )
    return prediction_powers, prediction_times, complexities

Выберите параметры#

Мы выбираем параметры для каждого из наших оценщиков, создавая словарь со всеми необходимыми значениями. changing_param является именем параметра, который будет варьироваться в каждом оценщике. Сложность будет определена complexity_label и рассчитывается с использованием complexity_computer. Also note that depending on the estimator type we are passing different data.

def _count_nonzero_coefficients(estimator):
    a = estimator.coef_.toarray()
    return np.count_nonzero(a)


configurations = [
    {
        "estimator": SGDClassifier,
        "tuned_params": {
            "penalty": "elasticnet",
            "alpha": 0.001,
            "loss": "modified_huber",
            "fit_intercept": True,
            "tol": 1e-1,
            "n_iter_no_change": 2,
        },
        "changing_param": "l1_ratio",
        "changing_param_values": [0.25, 0.5, 0.75, 0.9],
        "complexity_label": "non_zero coefficients",
        "complexity_computer": _count_nonzero_coefficients,
        "prediction_performance_computer": hamming_loss,
        "prediction_performance_label": "Hamming Loss (Misclassification Ratio)",
        "postfit_hook": lambda x: x.sparsify(),
        "data": classification_data,
        "n_samples": 5,
    },
    {
        "estimator": NuSVR,
        "tuned_params": {"C": 1e3, "gamma": 2**-15},
        "changing_param": "nu",
        "changing_param_values": [0.05, 0.1, 0.2, 0.35, 0.5],
        "complexity_label": "n_support_vectors",
        "complexity_computer": lambda x: len(x.support_vectors_),
        "data": regression_data,
        "postfit_hook": lambda x: x,
        "prediction_performance_computer": mean_squared_error,
        "prediction_performance_label": "MSE",
        "n_samples": 15,
    },
    {
        "estimator": GradientBoostingRegressor,
        "tuned_params": {
            "loss": "squared_error",
            "learning_rate": 0.05,
            "max_depth": 2,
        },
        "changing_param": "n_estimators",
        "changing_param_values": [10, 25, 50, 75, 100],
        "complexity_label": "n_trees",
        "complexity_computer": lambda x: x.n_estimators,
        "data": regression_data,
        "postfit_hook": lambda x: x,
        "prediction_performance_computer": mean_squared_error,
        "prediction_performance_label": "MSE",
        "n_samples": 15,
    },
]

Запустите код и постройте график результатов#

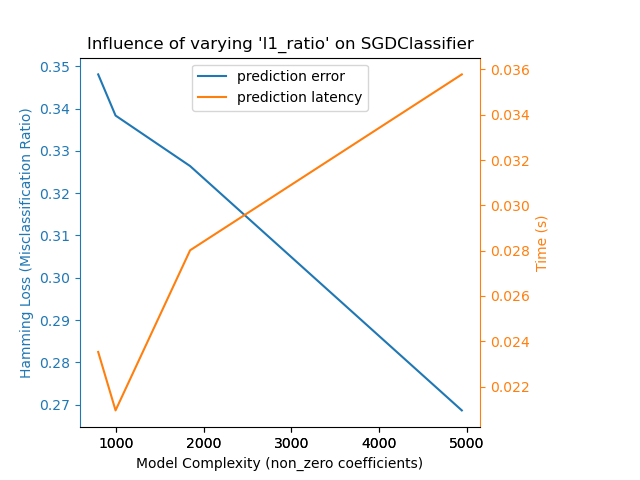
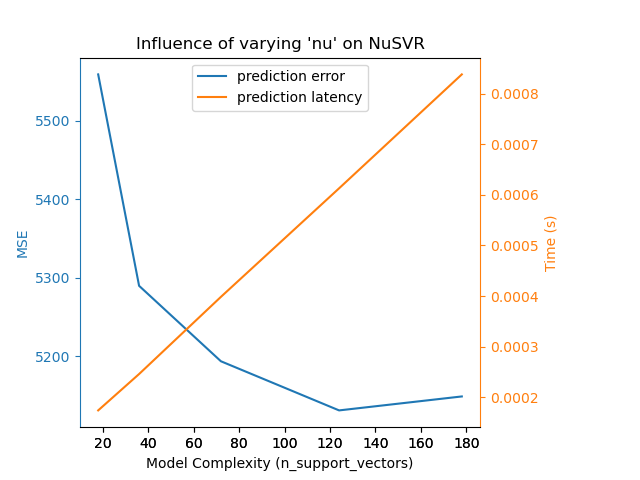
Мы определили все функции, необходимые для запуска нашего теста. Теперь мы пройдемся по различным конфигурациям, которые мы определили ранее. Затем мы можем проанализировать графики, полученные из теста: Ослабление L1 штраф в классификаторе SGD уменьшает ошибку предсказания, но приводит к увеличению времени обучения. Мы можем провести аналогичный анализ относительно времени обучения, которое увеличивается с количеством опорных векторов в Nu-SVR. Однако мы заметили, что существует оптимальное количество опорных векторов, которое уменьшает ошибку предсказания. Действительно, слишком мало опорных векторов приводит к недообученной модели, а слишком много опорных векторов приводит к переобученной модели. 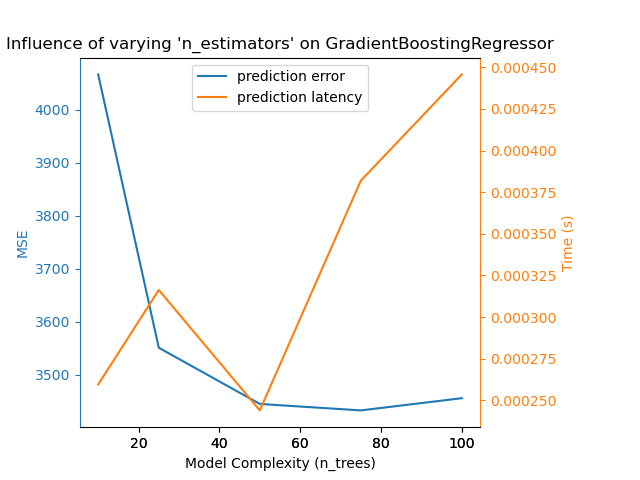Точно такой же вывод можно сделать для модели градиентного бустинга. Единственная разница с Nu-SVR заключается в том, что наличие слишком многих деревьев в ансамбле не так пагубно.

def plot_influence(conf, mse_values, prediction_times, complexities):
    """
    Plot influence of model complexity on both accuracy and latency.
    """

    fig = plt.figure()
    fig.subplots_adjust(right=0.75)

    # first axes (prediction error)
    ax1 = fig.add_subplot(111)
    line1 = ax1.plot(complexities, mse_values, c="tab:blue", ls="-")[0]
    ax1.set_xlabel("Model Complexity (%s)" % conf["complexity_label"])
    y1_label = conf["prediction_performance_label"]
    ax1.set_ylabel(y1_label)

    ax1.spines["left"].set_color(line1.get_color())
    ax1.yaxis.label.set_color(line1.get_color())
    ax1.tick_params(axis="y", colors=line1.get_color())

    # second axes (latency)
    ax2 = fig.add_subplot(111, sharex=ax1, frameon=False)
    line2 = ax2.plot(complexities, prediction_times, c="tab:orange", ls="-")[0]
    ax2.yaxis.tick_right()
    ax2.yaxis.set_label_position("right")
    y2_label = "Time (s)"
    ax2.set_ylabel(y2_label)
    ax1.spines["right"].set_color(line2.get_color())
    ax2.yaxis.label.set_color(line2.get_color())
    ax2.tick_params(axis="y", colors=line2.get_color())

    plt.legend(
        (line1, line2), ("prediction error", "prediction latency"), loc="upper center"
    )

    plt.title(
        "Influence of varying '%s' on %s"
        % (conf["changing_param"], conf["estimator"].__name__)
    )


for conf in configurations:
    prediction_performances, prediction_times, complexities = benchmark_influence(conf)
    plot_influence(conf, prediction_performances, prediction_times, complexities)
plt.show()

Benchmarking SGDClassifier(alpha=0.001, l1_ratio=0.25, loss='modified_huber',
              n_iter_no_change=2, penalty='elasticnet', tol=0.1)
Complexity: 4944 | Hamming Loss (Misclassification Ratio): 0.2687 | Pred. Time: 0.035781s

Benchmarking SGDClassifier(alpha=0.001, l1_ratio=0.5, loss='modified_huber',
              n_iter_no_change=2, penalty='elasticnet', tol=0.1)
Complexity: 1847 | Hamming Loss (Misclassification Ratio): 0.3264 | Pred. Time: 0.028017s

Benchmarking SGDClassifier(alpha=0.001, l1_ratio=0.75, loss='modified_huber',
              n_iter_no_change=2, penalty='elasticnet', tol=0.1)
Complexity: 997 | Hamming Loss (Misclassification Ratio): 0.3383 | Pred. Time: 0.020948s

Benchmarking SGDClassifier(alpha=0.001, l1_ratio=0.9, loss='modified_huber',
              n_iter_no_change=2, penalty='elasticnet', tol=0.1)
Complexity: 799 | Hamming Loss (Misclassification Ratio): 0.3481 | Pred. Time: 0.023528s

Benchmarking NuSVR(C=1000.0, gamma=3.0517578125e-05, nu=0.05)
Complexity: 18 | MSE: 5558.7313 | Pred. Time: 0.000174s

Benchmarking NuSVR(C=1000.0, gamma=3.0517578125e-05, nu=0.1)
Complexity: 36 | MSE: 5289.8022 | Pred. Time: 0.000246s

Benchmarking NuSVR(C=1000.0, gamma=3.0517578125e-05, nu=0.2)
Complexity: 72 | MSE: 5193.8353 | Pred. Time: 0.000398s

Benchmarking NuSVR(C=1000.0, gamma=3.0517578125e-05, nu=0.35)
Complexity: 124 | MSE: 5131.3279 | Pred. Time: 0.000613s

Benchmarking NuSVR(C=1000.0, gamma=3.0517578125e-05)
Complexity: 178 | MSE: 5149.0779 | Pred. Time: 0.000839s

Benchmarking GradientBoostingRegressor(learning_rate=0.05, max_depth=2, n_estimators=10)
Complexity: 10 | MSE: 4066.4812 | Pred. Time: 0.000260s

Benchmarking GradientBoostingRegressor(learning_rate=0.05, max_depth=2, n_estimators=25)
Complexity: 25 | MSE: 3551.1723 | Pred. Time: 0.000316s

Benchmarking GradientBoostingRegressor(learning_rate=0.05, max_depth=2, n_estimators=50)
Complexity: 50 | MSE: 3445.2171 | Pred. Time: 0.000244s

Benchmarking GradientBoostingRegressor(learning_rate=0.05, max_depth=2, n_estimators=75)
Complexity: 75 | MSE: 3433.0358 | Pred. Time: 0.000382s

Benchmarking GradientBoostingRegressor(learning_rate=0.05, max_depth=2)
Complexity: 100 | MSE: 3456.0602 | Pred. Time: 0.000446s

Заключение#

В заключение мы можем вывести следующие инсайты:

модель, которая является более сложной (или выразительной), потребует большего времени обучения;
более сложная модель не гарантирует уменьшения ошибки предсказания.

Эти аспекты связаны с обобщающей способностью модели и предотвращением недообучения или переобучения модели.

Общее время выполнения скрипта: (0 минут 6.007 секунд)

Связанные примеры

Градиентный бустинг для регрессии

Анализ вариации байесовской гауссовой смеси с априорным типом концентрации

Параметры SVM с RBF-ядром

Ранняя остановка в градиентном бустинге

Галерея, созданная Sphinx-Gallery

Влияние сложности модели#

Загрузить данные#

Влияние на бенчмарк#

Выберите параметры#

Запустите код и постройте график результатов#

Заключение#

Эта страница