Примечание
Перейти в конец чтобы скачать полный пример кода или запустить этот пример в браузере через JupyterLite или Binder.
Сравнение ядерной регрессии гребня и SVR#
Как регрессия гребня с ядром (KRR), так и SVR изучают нелинейную функцию, используя ядерный трюк, т.е. они изучают линейную функцию в пространстве, индуцированном соответствующим ядром, что соответствует нелинейной функции в исходном пространстве. Они различаются функциями потерь (гребневая потеря против эпсилон-нечувствительной потери). В отличие от SVR, подгонка KRR может быть выполнена в замкнутой форме и обычно быстрее для наборов данных среднего размера. С другой стороны, обученная модель не является разреженной и поэтому медленнее, чем SVR, во время предсказания.
Этот пример иллюстрирует оба метода на искусственном наборе данных, который состоит из синусоидальной целевой функции и сильного шума, добавленного к каждой пятой точке данных.
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
Сгенерировать тестовые данные#
import numpy as np
rng = np.random.RandomState(42)
X = 5 * rng.rand(10000, 1)
y = np.sin(X).ravel()
# Add noise to targets
y[::5] += 3 * (0.5 - rng.rand(X.shape[0] // 5))
X_plot = np.linspace(0, 5, 100000)[:, None]
Построить регрессионные модели на основе ядра#
from sklearn.kernel_ridge import KernelRidge
from sklearn.model_selection import GridSearchCV
from sklearn.svm import SVR
train_size = 100
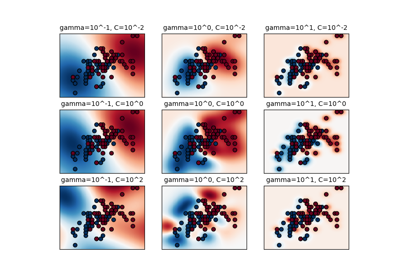
svr = GridSearchCV(
SVR(kernel="rbf", gamma=0.1),
param_grid={"C": [1e0, 1e1, 1e2, 1e3], "gamma": np.logspace(-2, 2, 5)},
)
kr = GridSearchCV(
KernelRidge(kernel="rbf", gamma=0.1),
param_grid={"alpha": [1e0, 0.1, 1e-2, 1e-3], "gamma": np.logspace(-2, 2, 5)},
)
Сравнение времени работы SVR и Kernel Ridge Regression#
import time
t0 = time.time()
svr.fit(X[:train_size], y[:train_size])
svr_fit = time.time() - t0
print(f"Best SVR with params: {svr.best_params_} and R2 score: {svr.best_score_:.3f}")
print("SVR complexity and bandwidth selected and model fitted in %.3f s" % svr_fit)
t0 = time.time()
kr.fit(X[:train_size], y[:train_size])
kr_fit = time.time() - t0
print(f"Best KRR with params: {kr.best_params_} and R2 score: {kr.best_score_:.3f}")
print("KRR complexity and bandwidth selected and model fitted in %.3f s" % kr_fit)
sv_ratio = svr.best_estimator_.support_.shape[0] / train_size
print("Support vector ratio: %.3f" % sv_ratio)
t0 = time.time()
y_svr = svr.predict(X_plot)
svr_predict = time.time() - t0
print("SVR prediction for %d inputs in %.3f s" % (X_plot.shape[0], svr_predict))
t0 = time.time()
y_kr = kr.predict(X_plot)
kr_predict = time.time() - t0
print("KRR prediction for %d inputs in %.3f s" % (X_plot.shape[0], kr_predict))
Best SVR with params: {'C': 1.0, 'gamma': np.float64(0.1)} and R2 score: 0.737
SVR complexity and bandwidth selected and model fitted in 0.514 s
Best KRR with params: {'alpha': 0.1, 'gamma': np.float64(0.1)} and R2 score: 0.723
KRR complexity and bandwidth selected and model fitted in 0.184 s
Support vector ratio: 0.340
SVR prediction for 100000 inputs in 0.116 s
KRR prediction for 100000 inputs in 0.617 s
Посмотрите на результаты#
import matplotlib.pyplot as plt
sv_ind = svr.best_estimator_.support_
plt.scatter(
X[sv_ind],
y[sv_ind],
c="r",
s=50,
label="SVR support vectors",
zorder=2,
edgecolors=(0, 0, 0),
)
plt.scatter(X[:100], y[:100], c="k", label="data", zorder=1, edgecolors=(0, 0, 0))
plt.plot(
X_plot,
y_svr,
c="r",
label="SVR (fit: %.3fs, predict: %.3fs)" % (svr_fit, svr_predict),
)
plt.plot(
X_plot, y_kr, c="g", label="KRR (fit: %.3fs, predict: %.3fs)" % (kr_fit, kr_predict)
)
plt.xlabel("data")
plt.ylabel("target")
plt.title("SVR versus Kernel Ridge")
_ = plt.legend()
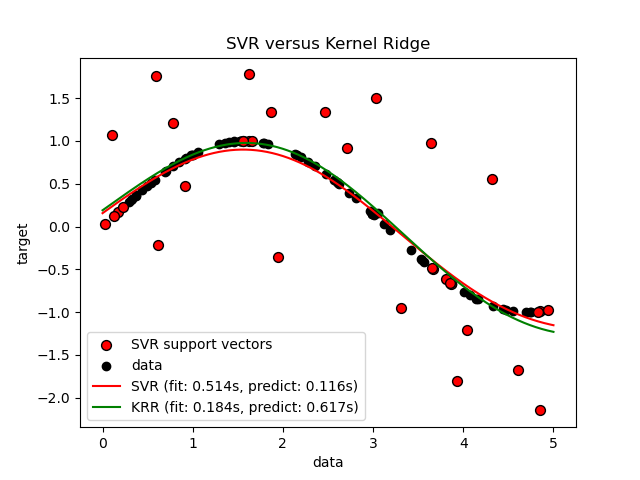
Предыдущий рисунок сравнивает обученную модель KRR и SVR, когда оба параметра сложности/регуляризации и ширины ядра RBF оптимизированы с использованием сеточного поиска. Обученные функции очень похожи; однако, обучение KRR приблизительно в 3-4 раза быстрее, чем обучение SVR (оба с сеточным поиском).
Предсказание 100000 целевых значений теоретически может быть примерно в три раза быстрее с SVR, поскольку он обучил разреженную модель, используя только примерно 1/3 точек обучающих данных в качестве опорных векторов. Однако на практике это не обязательно так из-за деталей реализации в способе вычисления функции ядра для каждой модели, что может сделать модель KRR такой же быстрой или даже быстрее, несмотря на выполнение большего количества арифметических операций.
Визуализация времени обучения и предсказания#
plt.figure()
sizes = np.logspace(1, 3.8, 7).astype(int)
for name, estimator in {
"KRR": KernelRidge(kernel="rbf", alpha=0.01, gamma=10),
"SVR": SVR(kernel="rbf", C=1e2, gamma=10),
}.items():
train_time = []
test_time = []
for train_test_size in sizes:
t0 = time.time()
estimator.fit(X[:train_test_size], y[:train_test_size])
train_time.append(time.time() - t0)
t0 = time.time()
estimator.predict(X_plot[:1000])
test_time.append(time.time() - t0)
plt.plot(
sizes,
train_time,
"o-",
color="r" if name == "SVR" else "g",
label="%s (train)" % name,
)
plt.plot(
sizes,
test_time,
"o--",
color="r" if name == "SVR" else "g",
label="%s (test)" % name,
)
plt.xscale("log")
plt.yscale("log")
plt.xlabel("Train size")
plt.ylabel("Time (seconds)")
plt.title("Execution Time")
_ = plt.legend(loc="best")
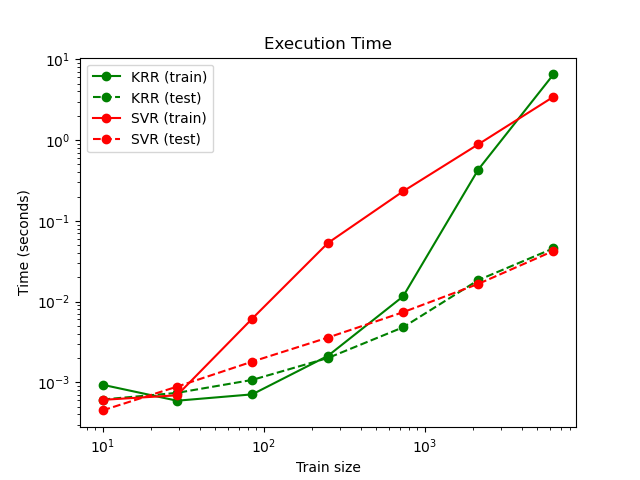
Этот график сравнивает время обучения и предсказания для KRR и SVR при различных размерах обучающей выборки. Обучение KRR быстрее, чем SVR для средних обучающих выборок (менее нескольких тысяч примеров); однако для больших выборок SVR масштабируется лучше. Что касается времени предсказания, SVR должен быть быстрее KRR для всех размеров обучающей выборки из-за обученного разреженного решения, но на практике это не всегда так из-за особенностей реализации. Обратите внимание, что степень разреженности и, следовательно, время предсказания зависят от параметров epsilon и C SVR.
Визуализировать кривые обучения#
from sklearn.model_selection import LearningCurveDisplay
_, ax = plt.subplots()
svr = SVR(kernel="rbf", C=1e1, gamma=0.1)
kr = KernelRidge(kernel="rbf", alpha=0.1, gamma=0.1)
common_params = {
"X": X[:100],
"y": y[:100],
"train_sizes": np.linspace(0.1, 1, 10),
"scoring": "neg_mean_squared_error",
"negate_score": True,
"score_name": "Mean Squared Error",
"score_type": "test",
"std_display_style": None,
"ax": ax,
}
LearningCurveDisplay.from_estimator(svr, **common_params)
LearningCurveDisplay.from_estimator(kr, **common_params)
ax.set_title("Learning curves")
ax.legend(handles=ax.get_legend_handles_labels()[0], labels=["SVR", "KRR"])
plt.show()
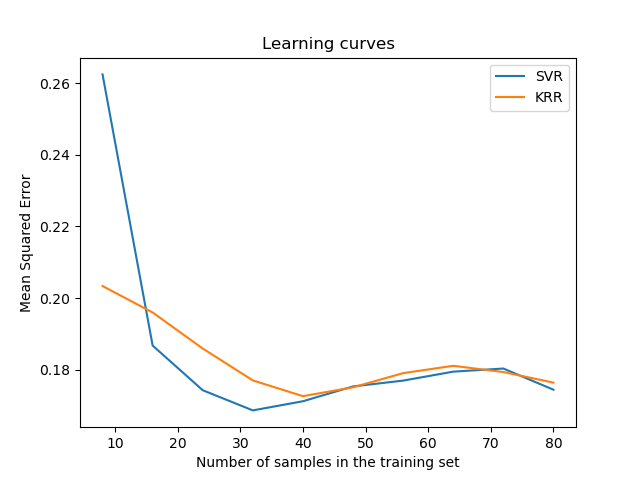
Общее время выполнения скрипта: (0 минут 13.777 секунд)
Связанные примеры
Регрессия на основе метода опорных векторов (SVR) с использованием линейных и нелинейных ядер
Вероятностные предсказания с гауссовским процессом классификации (GPC)
Пример распознавания лиц с использованием собственных лиц и SVM