Примечание
Перейти в конец чтобы скачать полный пример кода или запустить этот пример в браузере через JupyterLite или Binder.
Многометочная классификация#
Этот пример моделирует проблему классификации многометочных документов. Набор данных генерируется случайным образом на основе следующего процесса:
выбрать количество меток: n ~ Poisson(n_labels)
n раз, выберите класс c: c ~ Multinomial(theta)
выбрать длину документа: k ~ Poisson(length)
k раз, выбрать слово: w ~ Multinomial(theta_c)
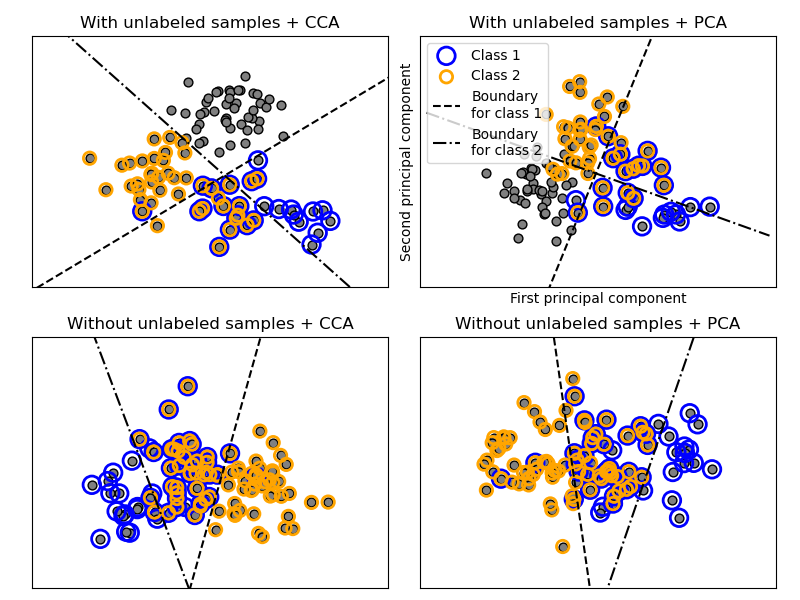
В описанном процессе используется отбраковочная выборка, чтобы убедиться, что n больше 2 и длина документа никогда не равна нулю. Аналогично, мы отбрасываем классы, которые уже были выбраны. Документы, назначенные обоим классам, отображаются окруженными двумя цветными кругами.
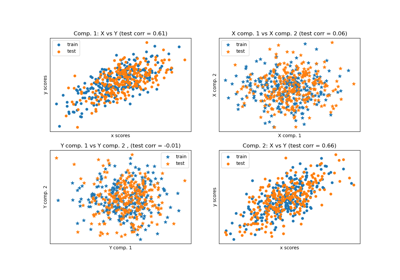
Классификация выполняется путем проекции на первые две главные
компоненты, найденные PCA и CCA для целей визуализации, с последующим использованием OneVsRestClassifier метаклассификатор, использующий два
SVC с линейными ядрами для обучения дискриминативной модели для каждого класса.
Обратите внимание, что PCA используется для выполнения неконтролируемого снижения размерности,
в то время как CCA используется для контролируемого.
Примечание: на графике "неразмеченные выборки" не означает, что мы не знаем метки (как в полуконтролируемом обучении), а что выборки просто не не имеют метку.
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
import matplotlib.pyplot as plt
import numpy as np
from sklearn.cross_decomposition import CCA
from sklearn.datasets import make_multilabel_classification
from sklearn.decomposition import PCA
from sklearn.multiclass import OneVsRestClassifier
from sklearn.svm import SVC
def plot_hyperplane(clf, min_x, max_x, linestyle, label):
# get the separating hyperplane
w = clf.coef_[0]
a = -w[0] / w[1]
xx = np.linspace(min_x - 5, max_x + 5) # make sure the line is long enough
yy = a * xx - (clf.intercept_[0]) / w[1]
plt.plot(xx, yy, linestyle, label=label)
def plot_subfigure(X, Y, subplot, title, transform):
if transform == "pca":
X = PCA(n_components=2).fit_transform(X)
elif transform == "cca":
X = CCA(n_components=2).fit(X, Y).transform(X)
else:
raise ValueError
min_x = np.min(X[:, 0])
max_x = np.max(X[:, 0])
min_y = np.min(X[:, 1])
max_y = np.max(X[:, 1])
classif = OneVsRestClassifier(SVC(kernel="linear"))
classif.fit(X, Y)
plt.subplot(2, 2, subplot)
plt.title(title)
zero_class = (Y[:, 0]).nonzero()
one_class = (Y[:, 1]).nonzero()
plt.scatter(X[:, 0], X[:, 1], s=40, c="gray", edgecolors=(0, 0, 0))
plt.scatter(
X[zero_class, 0],
X[zero_class, 1],
s=160,
edgecolors="b",
facecolors="none",
linewidths=2,
label="Class 1",
)
plt.scatter(
X[one_class, 0],
X[one_class, 1],
s=80,
edgecolors="orange",
facecolors="none",
linewidths=2,
label="Class 2",
)
plot_hyperplane(
classif.estimators_[0], min_x, max_x, "k--", "Boundary\nfor class 1"
)
plot_hyperplane(
classif.estimators_[1], min_x, max_x, "k-.", "Boundary\nfor class 2"
)
plt.xticks(())
plt.yticks(())
plt.xlim(min_x - 0.5 * max_x, max_x + 0.5 * max_x)
plt.ylim(min_y - 0.5 * max_y, max_y + 0.5 * max_y)
if subplot == 2:
plt.xlabel("First principal component")
plt.ylabel("Second principal component")
plt.legend(loc="upper left")
plt.figure(figsize=(8, 6))
X, Y = make_multilabel_classification(
n_classes=2, n_labels=1, allow_unlabeled=True, random_state=1
)
plot_subfigure(X, Y, 1, "With unlabeled samples + CCA", "cca")
plot_subfigure(X, Y, 2, "With unlabeled samples + PCA", "pca")
X, Y = make_multilabel_classification(
n_classes=2, n_labels=1, allow_unlabeled=False, random_state=1
)
plot_subfigure(X, Y, 3, "Without unlabeled samples + CCA", "cca")
plot_subfigure(X, Y, 4, "Without unlabeled samples + PCA", "pca")
plt.subplots_adjust(0.04, 0.02, 0.97, 0.94, 0.09, 0.2)
plt.show()
Общее время выполнения скрипта: (0 минут 0.154 секунды)
Связанные примеры

Построение случайно сгенерированного многометочного набора данных
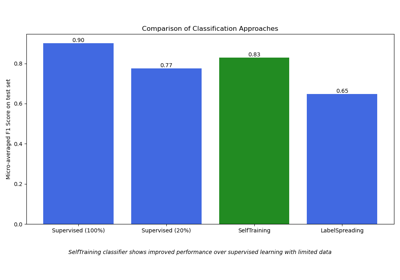
Полу-контролируемая классификация на текстовом наборе данных