Примечание

Перейти в конец чтобы скачать полный пример кода или запустить этот пример в браузере через JupyterLite или Binder.

Сравнение влияния различных масштабировщиков на данные с выбросами#

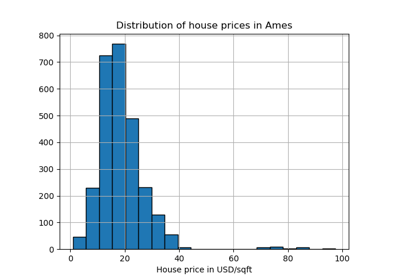
Признак 0 (медианный доход в блоке) и признак 5 (средняя заселённость домов) из California Housing dataset имеют очень разные масштабы и содержат некоторые очень большие выбросы. Эти две характеристики приводят к трудностям визуализации данных и, что более важно, они могут ухудшить прогностическую производительность многих алгоритмов машинного обучения. Неотмасштабированные данные также могут замедлить или даже предотвратить сходимость многих градиентных оценщиков.

Действительно, многие оценщики разработаны с предположением, что каждый признак принимает значения, близкие к нулю, или, что более важно, что все признаки изменяются в сопоставимых масштабах. В частности, метрические и градиентные оценщики часто предполагают приблизительно стандартизированные данные (центрированные признаки с единичными дисперсиями). Заметным исключением являются оценщики на основе деревьев решений, которые устойчивы к произвольному масштабированию данных.

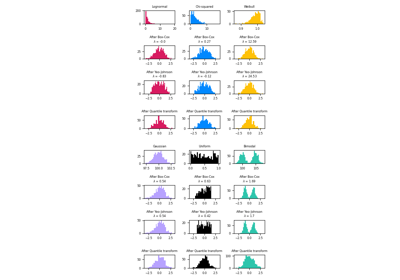
В этом примере используются различные масштабаторы, преобразователи и нормализаторы для приведения данных в предопределённый диапазон.

Скалеры являются линейными (или, точнее, аффинными) преобразователями и отличаются друг от друга способом оценки параметров, используемых для сдвига и масштабирования каждого признака.

QuantileTransformer предоставляет нелинейные преобразования, в которых расстояния между маргинальными выбросами и нормальными точками уменьшаются. PowerTransformer предоставляет нелинейные преобразования, в которых данные отображаются в нормальное распределение для стабилизации дисперсии и минимизации асимметрии.

В отличие от предыдущих преобразований, нормализация относится к преобразованию на каждый образец, а не на каждый признак.

Следующий код немного многословен, не стесняйтесь перейти непосредственно к анализу FeatureHasher на частотных словарях.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

import matplotlib as mpl
import numpy as np
from matplotlib import cm
from matplotlib import pyplot as plt

from sklearn.datasets import fetch_california_housing
from sklearn.preprocessing import (
    MaxAbsScaler,
    MinMaxScaler,
    Normalizer,
    PowerTransformer,
    QuantileTransformer,
    RobustScaler,
    StandardScaler,
    minmax_scale,
)

dataset = fetch_california_housing()
X_full, y_full = dataset.data, dataset.target
feature_names = dataset.feature_names

feature_mapping = {
    "MedInc": "Median income in block",
    "HouseAge": "Median house age in block",
    "AveRooms": "Average number of rooms",
    "AveBedrms": "Average number of bedrooms",
    "Population": "Block population",
    "AveOccup": "Average house occupancy",
    "Latitude": "House block latitude",
    "Longitude": "House block longitude",
}

# Take only 2 features to make visualization easier
# Feature MedInc has a long tail distribution.
# Feature AveOccup has a few but very large outliers.
features = ["MedInc", "AveOccup"]
features_idx = [feature_names.index(feature) for feature in features]
X = X_full[:, features_idx]
distributions = [
    ("Unscaled data", X),
    ("Data after standard scaling", StandardScaler().fit_transform(X)),
    ("Data after min-max scaling", MinMaxScaler().fit_transform(X)),
    ("Data after max-abs scaling", MaxAbsScaler().fit_transform(X)),
    (
        "Data after robust scaling",
        RobustScaler(quantile_range=(25, 75)).fit_transform(X),
    ),
    (
        "Data after power transformation (Yeo-Johnson)",
        PowerTransformer(method="yeo-johnson").fit_transform(X),
    ),
    (
        "Data after power transformation (Box-Cox)",
        PowerTransformer(method="box-cox").fit_transform(X),
    ),
    (
        "Data after quantile transformation (uniform pdf)",
        QuantileTransformer(
            output_distribution="uniform", random_state=42
        ).fit_transform(X),
    ),
    (
        "Data after quantile transformation (gaussian pdf)",
        QuantileTransformer(
            output_distribution="normal", random_state=42
        ).fit_transform(X),
    ),
    ("Data after sample-wise L2 normalizing", Normalizer().fit_transform(X)),
]

# scale the output between 0 and 1 for the colorbar
y = minmax_scale(y_full)

# plasma does not exist in matplotlib < 1.5
cmap = getattr(cm, "plasma_r", cm.hot_r)


def create_axes(title, figsize=(16, 6)):
    fig = plt.figure(figsize=figsize)
    fig.suptitle(title)

    # define the axis for the first plot
    left, width = 0.1, 0.22
    bottom, height = 0.1, 0.7
    bottom_h = height + 0.15
    left_h = left + width + 0.02

    rect_scatter = [left, bottom, width, height]
    rect_histx = [left, bottom_h, width, 0.1]
    rect_histy = [left_h, bottom, 0.05, height]

    ax_scatter = plt.axes(rect_scatter)
    ax_histx = plt.axes(rect_histx)
    ax_histy = plt.axes(rect_histy)

    # define the axis for the zoomed-in plot
    left = width + left + 0.2
    left_h = left + width + 0.02

    rect_scatter = [left, bottom, width, height]
    rect_histx = [left, bottom_h, width, 0.1]
    rect_histy = [left_h, bottom, 0.05, height]

    ax_scatter_zoom = plt.axes(rect_scatter)
    ax_histx_zoom = plt.axes(rect_histx)
    ax_histy_zoom = plt.axes(rect_histy)

    # define the axis for the colorbar
    left, width = width + left + 0.13, 0.01

    rect_colorbar = [left, bottom, width, height]
    ax_colorbar = plt.axes(rect_colorbar)

    return (
        (ax_scatter, ax_histy, ax_histx),
        (ax_scatter_zoom, ax_histy_zoom, ax_histx_zoom),
        ax_colorbar,
    )


def plot_distribution(axes, X, y, hist_nbins=50, title="", x0_label="", x1_label=""):
    ax, hist_X1, hist_X0 = axes

    ax.set_title(title)
    ax.set_xlabel(x0_label)
    ax.set_ylabel(x1_label)

    # The scatter plot
    colors = cmap(y)
    ax.scatter(X[:, 0], X[:, 1], alpha=0.5, marker="o", s=5, lw=0, c=colors)

    # Removing the top and the right spine for aesthetics
    # make nice axis layout
    ax.spines["top"].set_visible(False)
    ax.spines["right"].set_visible(False)
    ax.get_xaxis().tick_bottom()
    ax.get_yaxis().tick_left()
    ax.spines["left"].set_position(("outward", 10))
    ax.spines["bottom"].set_position(("outward", 10))

    # Histogram for axis X1 (feature 5)
    hist_X1.set_ylim(ax.get_ylim())
    hist_X1.hist(
        X[:, 1], bins=hist_nbins, orientation="horizontal", color="grey", ec="grey"
    )
    hist_X1.axis("off")

    # Histogram for axis X0 (feature 0)
    hist_X0.set_xlim(ax.get_xlim())
    hist_X0.hist(
        X[:, 0], bins=hist_nbins, orientation="vertical", color="grey", ec="grey"
    )
    hist_X0.axis("off")

Для каждого масштабировщика/нормализатора/преобразователя будут показаны два графика. Левый рисунок покажет диаграмму рассеяния полного набора данных, а правый рисунок исключит экстремальные значения, рассматривая только 99% набора данных, исключая маргинальные выбросы. Кроме того, маргинальные распределения для каждого признака будут показаны по бокам диаграммы рассеяния.

def make_plot(item_idx):
    title, X = distributions[item_idx]
    ax_zoom_out, ax_zoom_in, ax_colorbar = create_axes(title)
    axarr = (ax_zoom_out, ax_zoom_in)
    plot_distribution(
        axarr[0],
        X,
        y,
        hist_nbins=200,
        x0_label=feature_mapping[features[0]],
        x1_label=feature_mapping[features[1]],
        title="Full data",
    )

    # zoom-in
    zoom_in_percentile_range = (0, 99)
    cutoffs_X0 = np.percentile(X[:, 0], zoom_in_percentile_range)
    cutoffs_X1 = np.percentile(X[:, 1], zoom_in_percentile_range)

    non_outliers_mask = np.all(X > [cutoffs_X0[0], cutoffs_X1[0]], axis=1) & np.all(
        X < [cutoffs_X0[1], cutoffs_X1[1]], axis=1
    )
    plot_distribution(
        axarr[1],
        X[non_outliers_mask],
        y[non_outliers_mask],
        hist_nbins=50,
        x0_label=feature_mapping[features[0]],
        x1_label=feature_mapping[features[1]],
        title="Zoom-in",
    )

    norm = mpl.colors.Normalize(y_full.min(), y_full.max())
    mpl.colorbar.ColorbarBase(
        ax_colorbar,
        cmap=cmap,
        norm=norm,
        orientation="vertical",
        label="Color mapping for values of y",
    )

Исходные данные#

Каждое преобразование отображается с двумя преобразованными признаками, где левый график показывает весь набор данных, а правый увеличен, чтобы показать набор данных без выбросов на краях. Большинство образцов сжаты в определённый диапазон, [0, 10] для медианного дохода и [0, 6] для средней заселённости домов. Обратите внимание, что есть некоторые выбросы на краях (некоторые блоки имеют среднюю заселённость более 1200). Поэтому определённая предварительная обработка может быть очень полезной в зависимости от приложения. Далее мы представим некоторые инсайты и поведение этих методов предварительной обработки в присутствии выбросов на краях.

make_plot(0)

StandardScaler#

StandardScaler удаляет среднее значение и масштабирует данные до единичной дисперсии. Масштабирование сжимает диапазон значений признаков, как показано на левом рисунке ниже. Однако выбросы оказывают влияние при вычислении эмпирического среднего и стандартного отклонения. Обратите внимание, в частности, что поскольку выбросы для каждого признака имеют разную величину, разброс преобразованных данных для каждого признака очень различается: большинство данных лежат в диапазоне [-2, 4] для преобразованного признака медианного дохода, в то время как те же данные сжаты в меньшем диапазоне [-0.2, 0.2] для преобразованного признака средней заселенности домов.

StandardScaler поэтому не может гарантировать сбалансированные масштабы признаков при наличии выбросов.

make_plot(1)

Data after standard scaling, Full data, Zoom-in

MinMaxScaler#

MinMaxScaler масштабирует набор данных таким образом, что все значения признаков находятся в диапазоне [0, 1], как показано на правой панели ниже. Однако это масштабирование сжимает все инлайеры в узкий диапазон [0, 0.005] для преобразованной средней заселенности домов.

Оба StandardScaler и MinMaxScaler очень чувствительны к наличию выбросов.

make_plot(2)

Data after min-max scaling, Full data, Zoom-in

MaxAbsScaler#

MaxAbsScaler похож на MinMaxScaler за исключением того, что значения отображаются по нескольким диапазонам в зависимости от наличия отрицательных ИЛИ положительных значений. Если присутствуют только положительные значения, диапазон [0, 1]. Если присутствуют только отрицательные значения, диапазон [-1, 0]. Если присутствуют и отрицательные, и положительные значения, диапазон [-1, 1]. На данных только с положительными значениями, оба MinMaxScaler и MaxAbsScaler ведут себя аналогично. MaxAbsScaler поэтому также страдает от наличия больших выбросов.

make_plot(3)

Data after max-abs scaling, Full data, Zoom-in

RobustScaler#

В отличие от предыдущих масштабаторов, статистики центрирования и масштабирования RobustScaler основаны на процентилях и поэтому не подвержены влиянию небольшого количества очень больших выбросов по краям. Следовательно, результирующий диапазон преобразованных значений признаков больше, чем у предыдущих масштабаторов, и, что более важно, они приблизительно схожи: для обоих признаков большинство преобразованных значений лежит в диапазоне [-2, 3], как видно на увеличенном рисунке. Обратите внимание, что сами выбросы по-прежнему присутствуют в преобразованных данных. Если требуется отдельное отсечение выбросов, необходимо нелинейное преобразование (см. ниже).

make_plot(4)

Data after robust scaling, Full data, Zoom-in

PowerTransformer#

PowerTransformer применяет степенное преобразование к каждому признаку, чтобы сделать данные более похожими на гауссовы, для стабилизации дисперсии и минимизации асимметрии. В настоящее время поддерживаются преобразования Йео-Джонсона и Бокса-Кокса, а оптимальный масштабный коэффициент определяется с помощью оценки максимального правдоподобия в обоих методах. По умолчанию, PowerTransformer применяет нормализацию с нулевым средним и единичной дисперсией. Обратите внимание, что Box-Cox можно применять только к строго положительным данным. Доход и средняя заполняемость домов оказываются строго положительными, но если присутствуют отрицательные значения, предпочтительнее преобразование Yeo-Johnson.

make_plot(5)
make_plot(6)

QuantileTransformer (равномерный вывод)#

QuantileTransformer применяет нелинейное преобразование, такое что функция плотности вероятности каждого признака будет отображена на равномерное или распределение Гаусса. В этом случае все данные, включая выбросы, будут отображены на равномерное распределение в диапазоне [0, 1], делая выбросы неотличимыми от нормальных точек.

RobustScaler и QuantileTransformer устойчивы к выбросам в том смысле, что добавление или удаление выбросов в обучающем наборе даст приблизительно одинаковое преобразование. Но в отличие от RobustScaler, QuantileTransformer также автоматически сожмёт любые выбросы, установив их в заранее определённые границы диапазона (0 и 1). Это может привести к артефактам насыщения для экстремальных значений.

make_plot(7)

Data after quantile transformation (uniform pdf), Full data, Zoom-in

QuantileTransformer (Гауссовский вывод)#

Для отображения на гауссовское распределение установите параметр output_distribution='normal'.

make_plot(8)

Data after quantile transformation (gaussian pdf), Full data, Zoom-in

Нормализатор#

The Normalizer масштабирует вектор для каждой выборки до единичной нормы, независимо от распределения выборок. Это можно увидеть на обоих рисунках ниже, где все выборки отображаются на единичную окружность. В нашем примере две выбранные характеристики имеют только положительные значения; поэтому преобразованные данные лежат только в положительном квадранте. Это было бы не так, если бы некоторые исходные характеристики имели смесь положительных и отрицательных значений.