Статистическое сравнение моделей с использованием поиска по сетке

Этот пример иллюстрирует, как статистически сравнить производительность моделей, обученных и оцененных с использованием GridSearchCV.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

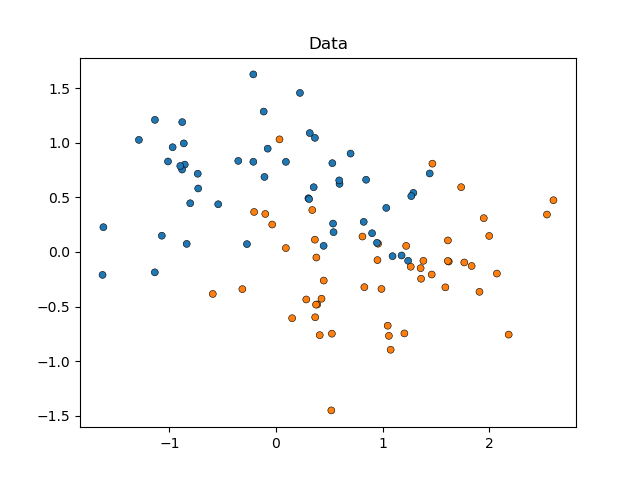
Мы начнем с моделирования данных в форме луны (где идеальное разделение между классами нелинейно), добавив к ним умеренный уровень шума. Точки данных будут принадлежать одному из двух возможных классов для прогнозирования двумя признаками. Мы смоделируем 50 образцов для каждого класса:

import matplotlib.pyplot as plt
import seaborn as sns

from sklearn.datasets import make_moons

X, y = make_moons(noise=0.352, random_state=1, n_samples=100)

sns.scatterplot(
    x=X[:, 0], y=X[:, 1], hue=y, marker="o", s=25, edgecolor="k", legend=False
).set_title("Data")
plt.show()

Мы сравним производительность SVC оценщики, которые различаются по своим kernel параметр, чтобы определить, какой выбор этого гиперпараметра лучше всего предсказывает наши смоделированные данные. Мы оценим производительность моделей с помощью RepeatedStratifiedKFold, повторяя 10 раз стратифицированную кросс-валидацию с 10 фолдами, используя различную рандомизацию данных в каждом повторении. Производительность будет оцениваться с помощью roc_auc_score.

from sklearn.model_selection import GridSearchCV, RepeatedStratifiedKFold
from sklearn.svm import SVC

param_grid = [
    {"kernel": ["linear"]},
    {"kernel": ["poly"], "degree": [2, 3]},
    {"kernel": ["rbf"]},
]

svc = SVC(random_state=0)

cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=10, random_state=0)

search = GridSearchCV(estimator=svc, param_grid=param_grid, scoring="roc_auc", cv=cv)
search.fit(X, y)

GridSearchCV(cv=RepeatedStratifiedKFold(n_repeats=10, n_splits=10, random_state=0),
             estimator=SVC(random_state=0),
             param_grid=[{'kernel': ['linear']},
                         {'degree': [2, 3], 'kernel': ['poly']},
                         {'kernel': ['rbf']}],
             scoring='roc_auc')

В среде Jupyter, пожалуйста, перезапустите эту ячейку, чтобы показать HTML-представление, или доверьтесь блокноту.
На GitHub HTML-представление не может отображаться, попробуйте загрузить эту страницу с помощью nbviewer.org.

Теперь мы можем проверить результаты нашего поиска, отсортированные по их mean_test_score:

import pandas as pd

results_df = pd.DataFrame(search.cv_results_)
results_df = results_df.sort_values(by=["rank_test_score"])
results_df = results_df.set_index(
    results_df["params"].apply(lambda x: "_".join(str(val) for val in x.values()))
).rename_axis("kernel")
results_df[["params", "rank_test_score", "mean_test_score", "std_test_score"]]

	params	rank_test_score	mean_test_score	std_test_score
ядро
rbf	{'kernel': 'rbf'}	1	0.9400	0.079297
линейный	{'kernel': 'linear'}	2	0.9300	0.077846
3_poly	{'degree': 3, 'kernel': 'poly'}	3	0.9044	0.098776
2_poly	{'degree': 2, 'kernel': 'poly'}	4	0.6852	0.169106

Мы видим, что оценщик, использующий 'rbf' ядро показало наилучший результат, за ним следует 'linear'. Оба оценщика с 'poly' ядро показало худшие результаты, при этом использование полинома второй степени дало гораздо более низкую производительность, чем все другие модели.

Обычно анализ на этом заканчивается, но половина истории отсутствует. Вывод GridSearchCV не предоставляет информацию об уверенности в различиях между моделями. Мы не знаем, являются ли эти статистически значимым. Чтобы оценить это, нам нужно провести статистический тест. В частности, чтобы сравнить производительность двух моделей, мы должны статистически сравнить их AUC-оценки. Есть 100 выборок (AUC-оценок) для каждой модели, так как мы повторили 10 раз 10-кратную перекрестную проверку.

Однако оценки моделей не являются независимыми: все модели оцениваются на тот же 100 разделов, увеличивая корреляцию между производительностью моделей. Поскольку некоторые разделы данных могут сделать различение классов особенно легким или трудным для всех моделей, оценки моделей будут ковариировать.

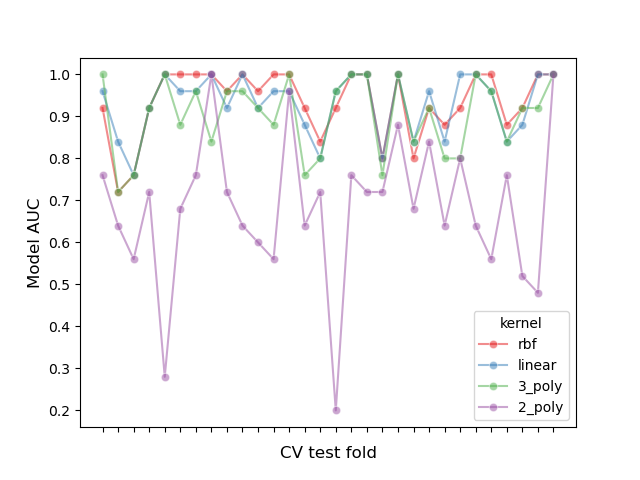
Давайте исследуем этот эффект разделения, построив график производительности всех моделей в каждом фолде и вычислив корреляцию между моделями по фолдам:

# create df of model scores ordered by performance
model_scores = results_df.filter(regex=r"split\d*_test_score")

# plot 30 examples of dependency between cv fold and AUC scores
fig, ax = plt.subplots()
sns.lineplot(
    data=model_scores.transpose().iloc[:30],
    dashes=False,
    palette="Set1",
    marker="o",
    alpha=0.5,
    ax=ax,
)
ax.set_xlabel("CV test fold", size=12, labelpad=10)
ax.set_ylabel("Model AUC", size=12)
ax.tick_params(bottom=True, labelbottom=False)
plt.show()

# print correlation of AUC scores across folds
print(f"Correlation of models:\n {model_scores.transpose().corr()}")

Correlation of models:
 kernel       rbf    linear    3_poly    2_poly
kernel
rbf     1.000000  0.882561  0.783392  0.351390
linear  0.882561  1.000000  0.746492  0.298688
3_poly  0.783392  0.746492  1.000000  0.355440
2_poly  0.351390  0.298688  0.355440  1.000000

Мы можем наблюдать, что производительность моделей сильно зависит от фолда.

Как следствие, если мы предположим независимость между выборками, мы будем недооценивать дисперсию, вычисленную в наших статистических тестах, увеличивая количество ложноположительных ошибок (т.е. обнаружение значимой разницы между моделями, когда такой разницы не существует) [1].

Для этих случаев были разработаны несколько статистических тестов с коррекцией дисперсии. В этом примере мы покажем, как реализовать один из них (так называемый скорректированный t-тест Надо и Бенжио) в рамках двух различных статистических подходов: частотного и байесовского.

Сравнение двух моделей: частотный подход

Мы можем начать с вопроса: «Значительно ли первая модель лучше второй модели (при ранжировании по mean_test_score)?

Чтобы ответить на этот вопрос с использованием частотного подхода, можно провести парный t-тест и вычислить p-значение. Это также известно как тест Дибольда-Мариано в литературе по прогнозированию. [5]. Многие варианты такого t-критерия были разработаны для учёта проблемы 'независимости выборок', описанной в предыдущем разделе. Мы будем использовать тот, который доказал получение наивысших показателей воспроизводимости (которые оценивают, насколько схожа производительность модели при её оценке на разных случайных разбиениях одного и того же набора данных), сохраняя при этом низкий уровень ложноположительных и ложноотрицательных результатов: скорректированный t-критерий Надо и Бенжио [2] который использует 10-кратно повторенную 10-кратную перекрестную проверку [3].

Этот скорректированный парный t-тест вычисляется как:

\[t=\frac{\frac{1}{k \cdot r}\sum_{i=1}^{k}\sum_{j=1}^{r}x_{ij}} {\sqrt{(\frac{1}{k \cdot r}+\frac{n_{test}}{n_{train}})\hat{\sigma}^2}}\]

где \(k\) это количество фолдов, \(r\) количество повторений в перекрестной проверке, \(x\) разница в производительности моделей, \(n_{test}\) это количество образцов, используемых для тестирования, \(n_{train}\) — это количество образцов, используемых для обучения, и \(\hat{\sigma}^2\) представляет дисперсию наблюдаемых различий.

Давайте реализуем исправленный правосторонний парный t-тест, чтобы оценить, является ли производительность первой модели значительно лучше, чем у второй модели. Наша нулевая гипотеза заключается в том, что вторая модель работает как минимум так же хорошо, как и первая.

import numpy as np
from scipy.stats import t


def corrected_std(differences, n_train, n_test):
    """Corrects standard deviation using Nadeau and Bengio's approach.

    Parameters
    ----------
    differences : ndarray of shape (n_samples,)
        Vector containing the differences in the score metrics of two models.
    n_train : int
        Number of samples in the training set.
    n_test : int
        Number of samples in the testing set.

    Returns
    -------
    corrected_std : float
        Variance-corrected standard deviation of the set of differences.
    """
    # kr = k times r, r times repeated k-fold crossvalidation,
    # kr equals the number of times the model was evaluated
    kr = len(differences)
    corrected_var = np.var(differences, ddof=1) * (1 / kr + n_test / n_train)
    corrected_std = np.sqrt(corrected_var)
    return corrected_std


def compute_corrected_ttest(differences, df, n_train, n_test):
    """Computes right-tailed paired t-test with corrected variance.

    Parameters
    ----------
    differences : array-like of shape (n_samples,)
        Vector containing the differences in the score metrics of two models.
    df : int
        Degrees of freedom.
    n_train : int
        Number of samples in the training set.
    n_test : int
        Number of samples in the testing set.

    Returns
    -------
    t_stat : float
        Variance-corrected t-statistic.
    p_val : float
        Variance-corrected p-value.
    """
    mean = np.mean(differences)
    std = corrected_std(differences, n_train, n_test)
    t_stat = mean / std
    p_val = t.sf(np.abs(t_stat), df)  # right-tailed t-test
    return t_stat, p_val

model_1_scores = model_scores.iloc[0].values  # scores of the best model
model_2_scores = model_scores.iloc[1].values  # scores of the second-best model

differences = model_1_scores - model_2_scores

n = differences.shape[0]  # number of test sets
df = n - 1
n_train = len(next(iter(cv.split(X, y)))[0])
n_test = len(next(iter(cv.split(X, y)))[1])

t_stat, p_val = compute_corrected_ttest(differences, df, n_train, n_test)
print(f"Corrected t-value: {t_stat:.3f}\nCorrected p-value: {p_val:.3f}")

Corrected t-value: 0.750
Corrected p-value: 0.227

Мы можем сравнить скорректированные t- и p-значения с нескорректированными:

t_stat_uncorrected = np.mean(differences) / np.sqrt(np.var(differences, ddof=1) / n)
p_val_uncorrected = t.sf(np.abs(t_stat_uncorrected), df)

print(
    f"Uncorrected t-value: {t_stat_uncorrected:.3f}\n"
    f"Uncorrected p-value: {p_val_uncorrected:.3f}"
)

Uncorrected t-value: 2.611
Uncorrected p-value: 0.005

Используя обычный уровень значимости alpha на p=0.05, мы наблюдаем, что нескорректированный t-тест делает вывод, что первая модель значительно лучше второй.

С исправленным подходом, напротив, мы не обнаруживаем эту разницу.

Однако в последнем случае частотный подход не позволяет нам сделать вывод, что первая и вторая модели имеют эквивалентную производительность. Если мы хотим сделать это утверждение, нам нужно использовать байесовский подход.

Сравнение двух моделей: байесовский подход

Мы можем использовать байесовскую оценку для вычисления вероятности того, что первая модель лучше второй. Байесовская оценка выведет распределение, за которым следует среднее \(\mu\) различий в производительности двух моделей.

Чтобы получить апостериорное распределение, нам нужно определить априорное распределение, которое моделирует наши представления о том, как распределено среднее значение до просмотра данных, и умножить его на функцию правдоподобия, которая вычисляет, насколько вероятны наблюдаемые различия, учитывая значения, которые может принимать среднее значение различий.

Байесовская оценка может быть выполнена во многих формах для ответа на наш вопрос, но в этом примере мы реализуем подход, предложенный Benavoli и коллегами [4].

Один из способов определения нашего апостериорного распределения с использованием замкнутого выражения — выбрать сопряженное априорное распределение для функции правдоподобия. Бенаволи и коллеги [4] показывают, что при сравнении производительности двух классификаторов мы можем смоделировать априорное распределение как нормально-гамма распределение (с неизвестными средним и дисперсией) сопряженное с нормальным правдоподобием, чтобы таким образом выразить апостериорное как нормальное распределение. Маргинализируя дисперсию из этого нормального апостериорного распределения, мы можем определить апостериорное распределение параметра среднего как t-распределение Стьюдента. Конкретно:

\[St(\mu;n-1,\overline{x},(\frac{1}{n}+\frac{n_{test}}{n_{train}}) \hat{\sigma}^2)\]

где \(n\) — это общее количество выборок, \(\overline{x}\) представляет среднюю разницу в оценках, \(n_{test}\) это количество образцов, используемых для тестирования, \(n_{train}\) — это количество образцов, используемых для обучения, и \(\hat{\sigma}^2\) представляет дисперсию наблюдаемых различий.

Обратите внимание, что мы используем скорректированную дисперсию Надо и Бенжио в нашем Байесовском подходе.

Давайте вычислим и построим апостериорное распределение:

# initialize random variable
t_post = t(
    df, loc=np.mean(differences), scale=corrected_std(differences, n_train, n_test)
)

Построим апостериорное распределение:

x = np.linspace(t_post.ppf(0.001), t_post.ppf(0.999), 100)

plt.plot(x, t_post.pdf(x))
plt.xticks(np.arange(-0.04, 0.06, 0.01))
plt.fill_between(x, t_post.pdf(x), 0, facecolor="blue", alpha=0.2)
plt.ylabel("Probability density")
plt.xlabel(r"Mean difference ($\mu$)")
plt.title("Posterior distribution")
plt.show()

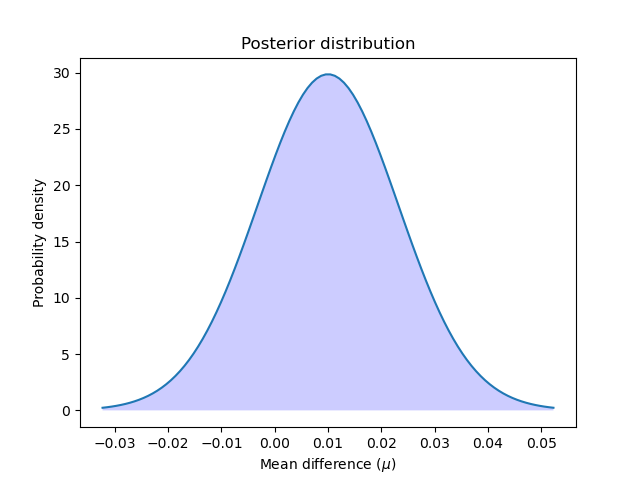
Мы можем рассчитать вероятность того, что первая модель лучше второй, вычислив площадь под кривой апостериорного распределения от нуля до бесконечности. И наоборот: мы можем рассчитать вероятность того, что вторая модель лучше первой, вычислив площадь под кривой от минус бесконечности до нуля.

better_prob = 1 - t_post.cdf(0)

print(
    f"Probability of {model_scores.index[0]} being more accurate than "
    f"{model_scores.index[1]}: {better_prob:.3f}"
)
print(
    f"Probability of {model_scores.index[1]} being more accurate than "
    f"{model_scores.index[0]}: {1 - better_prob:.3f}"
)

Probability of rbf being more accurate than linear: 0.773
Probability of linear being more accurate than rbf: 0.227

В отличие от частотного подхода, мы можем вычислить вероятность того, что одна модель лучше другой.

Обратите внимание, что мы получили результаты, аналогичные тем, что в частотном подходе. Учитывая наш выбор априорных распределений, мы по сути выполняем те же вычисления, но можем делать другие утверждения.

Область практической эквивалентности

Иногда нас интересует определение вероятностей того, что наши модели имеют эквивалентную производительность, где "эквивалентность" определяется практическим способом. Наивный подход [4] будет определять оценщики как практически эквивалентные, когда они отличаются менее чем на 1% по точности. Но мы также могли бы определить эту практическую эквивалентность с учетом решаемой задачи. Например, разница в 5% по точности означала бы увеличение продаж на $1000, и мы считаем любую величину выше этого релевантной для нашего бизнеса.

В этом примере мы определим Область Практической Эквивалентности (ROPE) как \([-0.01, 0.01]\). That is, we will consider two models as practically equivalent if they differ by less than 1% in their performance.

Чтобы вычислить вероятности практической эквивалентности классификаторов, мы рассчитываем площадь под кривой апостериорного распределения в интервале ROPE:

rope_interval = [-0.01, 0.01]
rope_prob = t_post.cdf(rope_interval[1]) - t_post.cdf(rope_interval[0])

print(
    f"Probability of {model_scores.index[0]} and {model_scores.index[1]} "
    f"being practically equivalent: {rope_prob:.3f}"
)

Probability of rbf and linear being practically equivalent: 0.432

Мы можем построить, как апостериорное распределение распределено по интервалу ROPE:

x_rope = np.linspace(rope_interval[0], rope_interval[1], 100)

plt.plot(x, t_post.pdf(x))
plt.xticks(np.arange(-0.04, 0.06, 0.01))
plt.vlines([-0.01, 0.01], ymin=0, ymax=(np.max(t_post.pdf(x)) + 1))
plt.fill_between(x_rope, t_post.pdf(x_rope), 0, facecolor="blue", alpha=0.2)
plt.ylabel("Probability density")
plt.xlabel(r"Mean difference ($\mu$)")
plt.title("Posterior distribution under the ROPE")
plt.show()

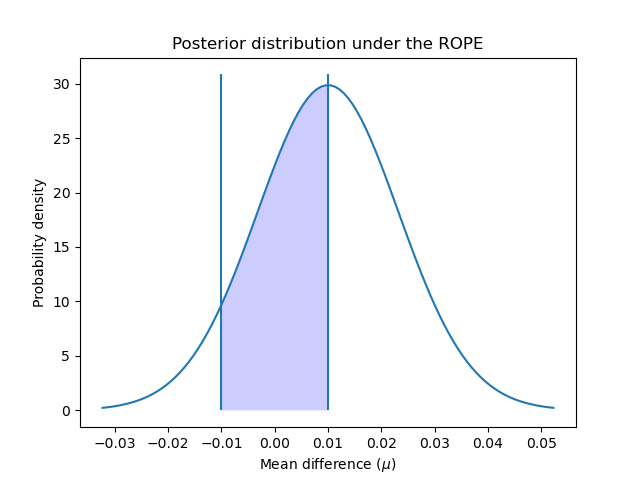
Как предложено в [4], мы можем дополнительно интерпретировать эти вероятности, используя те же критерии, что и частотный подход: вероятность попадания внутрь ROPE больше 95% (уровень значимости 5%)? В этом случае мы можем заключить, что обе модели практически эквивалентны.

Байесовский подход к оценке также позволяет нам вычислить, насколько мы не уверены в нашей оценке разницы. Это можно рассчитать с помощью достоверных интервалов. Для заданной вероятности они показывают диапазон значений, которые может принимать оцениваемая величина, в нашем случае средняя разница в производительности. Например, 50% достоверный интервал [x, y] говорит нам, что существует 50% вероятность того, что истинная (средняя) разница в производительности между моделями находится между x и y.

Определим доверительные интервалы наших данных, используя 50%, 75% и 95%:

cred_intervals = []
intervals = [0.5, 0.75, 0.95]

for interval in intervals:
    cred_interval = list(t_post.interval(interval))
    cred_intervals.append([interval, cred_interval[0], cred_interval[1]])

cred_int_df = pd.DataFrame(
    cred_intervals, columns=["interval", "lower value", "upper value"]
).set_index("interval")
cred_int_df

	нижнее значение	верхнее значение
интервал
0.50	0.000977	0.019023
0.75	-0.005422	0.025422
0.95	-0.016445	0.036445

Как показано в таблице, существует 50% вероятность того, что истинная средняя разница между моделями будет находиться между 0.000977 и 0.019023, 70% вероятность того, что она будет между -0.005422 и 0.025422, и 95% вероятность того, что она будет между -0.016445 и 0.036445.

Попарное сравнение всех моделей: частотный подход

Мы также могли бы быть заинтересованы в сравнении производительности всех наших моделей, оценённых с GridSearchCV. В этом случае мы будем запускать наш статистический тест несколько раз, что приводит нас к проблема множественных сравнений.

Существует много возможных способов решения этой проблемы, но стандартный подход — применить Поправка Бонферрони. Bonferroni может быть вычислен путём умножения p-значения на количество сравнений, которые мы тестируем.

Давайте сравним производительность моделей с использованием скорректированного t-теста:

from itertools import combinations
from math import factorial

n_comparisons = factorial(len(model_scores)) / (
    factorial(2) * factorial(len(model_scores) - 2)
)
pairwise_t_test = []

for model_i, model_k in combinations(range(len(model_scores)), 2):
    model_i_scores = model_scores.iloc[model_i].values
    model_k_scores = model_scores.iloc[model_k].values
    differences = model_i_scores - model_k_scores
    t_stat, p_val = compute_corrected_ttest(differences, df, n_train, n_test)
    p_val *= n_comparisons  # implement Bonferroni correction
    # Bonferroni can output p-values higher than 1
    p_val = 1 if p_val > 1 else p_val
    pairwise_t_test.append(
        [model_scores.index[model_i], model_scores.index[model_k], t_stat, p_val]
    )

pairwise_comp_df = pd.DataFrame(
    pairwise_t_test, columns=["model_1", "model_2", "t_stat", "p_val"]
).round(3)
pairwise_comp_df

	model_1	model_2	t_стат	p_val
0	rbf	линейный	0.750	1.000
1	rbf	3_poly	1.657	0.302
2	rbf	2_poly	4.565	0.000
3	линейный	3_poly	1.111	0.807
4	линейный	2_poly	4.276	0.000
5	3_poly	2_poly	3.851	0.001

Мы наблюдаем, что после корректировки на множественные сравнения единственная модель, которая значительно отличается от других, — это '2_poly'. 'rbf', модель, занявшая первое место по GridSearchCV, незначительно не отличается от 'linear' или '3_poly'.

Попарное сравнение всех моделей: байесовский подход

При использовании байесовской оценки для сравнения нескольких моделей нам не нужно корректировать множественные сравнения (по причинам, см. [4]).

Мы можем провести попарные сравнения тем же способом, что и в первом разделе:

pairwise_bayesian = []

for model_i, model_k in combinations(range(len(model_scores)), 2):
    model_i_scores = model_scores.iloc[model_i].values
    model_k_scores = model_scores.iloc[model_k].values
    differences = model_i_scores - model_k_scores
    t_post = t(
        df, loc=np.mean(differences), scale=corrected_std(differences, n_train, n_test)
    )
    worse_prob = t_post.cdf(rope_interval[0])
    better_prob = 1 - t_post.cdf(rope_interval[1])
    rope_prob = t_post.cdf(rope_interval[1]) - t_post.cdf(rope_interval[0])

    pairwise_bayesian.append([worse_prob, better_prob, rope_prob])

pairwise_bayesian_df = pd.DataFrame(
    pairwise_bayesian, columns=["worse_prob", "better_prob", "rope_prob"]
).round(3)

pairwise_comp_df = pairwise_comp_df.join(pairwise_bayesian_df)
pairwise_comp_df

	model_1	model_2	t_стат	p_val	worse_prob	better_prob	rope_prob
0	rbf	линейный	0.750	1.000	0.068	0.500	0.432
1	rbf	3_poly	1.657	0.302	0.018	0.882	0.100
2	rbf	2_poly	4.565	0.000	0.000	1.000	0.000
3	линейный	3_poly	1.111	0.807	0.063	0.750	0.187
4	линейный	2_poly	4.276	0.000	0.000	1.000	0.000
5	3_poly	2_poly	3.851	0.001	0.000	1.000	0.000

Используя байесовский подход, мы можем вычислить вероятность того, что модель работает лучше, хуже или практически эквивалентно другой.

Результаты показывают, что модель, занявшая первое место по GridSearchCV 'rbf', имеет приблизительно 6.8% шанс быть хуже, чем 'linear', и 1.8% вероятность быть хуже, чем '3_poly'. 'rbf' и 'linear' имеют 43% вероятность быть практически эквивалентными, в то время как 'rbf' и '3_poly' имеют 10% шанс быть таковыми.

Аналогично выводам, полученным с использованием частотного подхода, все модели имеют 100% вероятность быть лучше, чем '2_poly', и ни один из них не имеет практически эквивалентной производительности с последним.

Ключевые выводы

• Небольшие различия в показателях производительности могут легко оказаться случайными, а не потому, что одна модель предсказывает систематически лучше другой. Как показано в этом примере, статистика может сказать, насколько это вероятно.

• При статистическом сравнении производительности двух моделей, оцененных в GridSearchCV, необходимо скорректировать рассчитанную дисперсию, которая может быть недооценена, поскольку оценки моделей не являются независимыми друг от друга.

• Частотный подход, использующий (скорректированный по дисперсии) парный t-тест, может сказать нам, является ли производительность одной модели лучше другой с степенью уверенности выше случайной.

• Байесовский подход может предоставить вероятности того, что одна модель лучше, хуже или практически эквивалентна другой. Он также может сказать нам, насколько мы уверены в том, что истинные различия наших моделей попадают в определенный диапазон значений.

• При статистическом сравнении нескольких моделей требуется коррекция множественных сравнений при использовании частотного подхода.

Ссылки

[1]

Dietterich, T. G. (1998). Приближенные статистические тесты для сравнения алгоритмов обучения с учителем для классификацииNeural computation, 10(7).

[2]

Nadeau, C., & Bengio, Y. (2000). Оценка ошибки обобщения. В Advances in neural information processing systems.

[3]

Bouckaert, R. R., & Frank, E. (2004). Оценка воспроизводимости тестов значимости для сравнения алгоритмов обучения. На Тихоокеанско-Азиатской конференции по обнаружению знаний и интеллектуальному анализу данных.

[4] (1,2,3,4,5)

Benavoli, A., Corani, G., Demšar, J., & Zaffalon, M. (2017). Время для перемен: руководство по сравнению нескольких классификаторов с помощью байесовского анализа. Журнал исследований машинного обучения, 18(1). См. библиотеку Python, сопровождающую эту статью здесь.

[5]

Diebold, F.X. & Mariano R.S. (1995). Сравнение прогностической точности Journal of Business & economic statistics, 20(1), 134-144.

Связанные примеры

Тест с перестановками для значимости оценки классификации

Тест с перестановками для значимости оценки классификации

Сравнение калибровки классификаторов

Сравнение калибровки классификаторов

Распространённые ошибки в интерпретации коэффициентов линейных моделей

Распространённые ошибки в интерпретации коэффициентов линейных моделей

Примерный пайплайн для извлечения и оценки текстовых признаков

Примерный пайплайн для извлечения и оценки текстовых признаков