Примечание

Перейти в конец чтобы скачать полный пример кода или запустить этот пример в браузере через JupyterLite или Binder.

Регрессия на главных компонентах против регрессии методом частичных наименьших квадратов#

Этот пример сравнивает Регрессия на главных компонентах (PCR) и Регрессия методом частичных наименьших квадратов (PLS) на игрушечном наборе данных. Наша цель — проиллюстрировать, как PLS может превзойти PCR, когда цель сильно коррелирует с некоторыми направлениями в данных, имеющими низкую дисперсию.

PCR — это регрессор, состоящий из двух шагов: сначала, PCA применяется к обучающим данным, возможно, выполняя уменьшение размерности; затем, регрессор (например, линейный регрессор) обучается на преобразованных образцах. В PCA, преобразование является чисто неконтролируемым, то есть информация о целевых переменных не используется. В результате PCR может плохо работать в некоторых наборах данных, где цель сильно коррелирует с направления которые имеют низкую дисперсию. Действительно, снижение размерности PCA проецирует данные в пространство меньшей размерности, где дисперсия спроецированных данных жадно максимизируется вдоль каждой оси. Несмотря на то, что они имеют наибольшую предсказательную силу для целевой переменной, направления с меньшей дисперсией будут отброшены, и окончательный регрессор не сможет их использовать.

PLS является одновременно преобразователем и регрессором и очень похож на PCR: он также применяет уменьшение размерности к выборкам перед применением линейного регрессора к преобразованным данным. Основное отличие от PCR заключается в том, что преобразование PLS является контролируемым. Поэтому, как мы увидим в этом примере, оно не страдает от упомянутой выше проблемы.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

Данные#

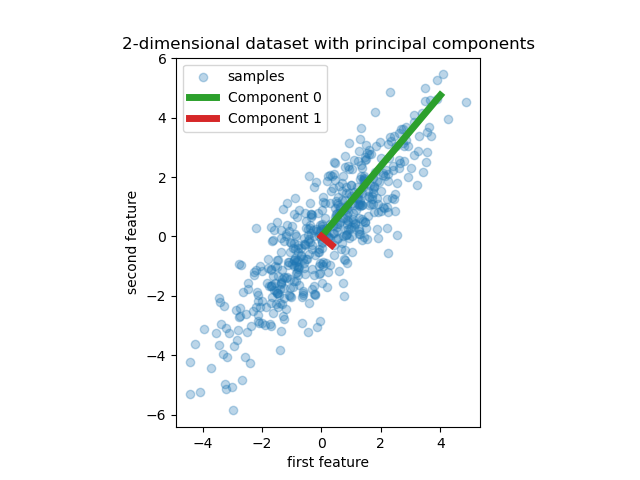
Мы начинаем с создания простого набора данных с двумя признаками. Прежде чем углубиться в PCR и PLS, мы подгоняем оценщик PCA, чтобы отобразить две главные компоненты этого набора данных, т.е. два направления, которые объясняют наибольшую дисперсию в данных.

import matplotlib.pyplot as plt
import numpy as np

from sklearn.decomposition import PCA

rng = np.random.RandomState(0)
n_samples = 500
cov = [[3, 3], [3, 4]]
X = rng.multivariate_normal(mean=[0, 0], cov=cov, size=n_samples)
pca = PCA(n_components=2).fit(X)


plt.scatter(X[:, 0], X[:, 1], alpha=0.3, label="samples")
for i, (comp, var) in enumerate(zip(pca.components_, pca.explained_variance_)):
    comp = comp * var  # scale component by its variance explanation power
    plt.plot(
        [0, comp[0]],
        [0, comp[1]],
        label=f"Component {i}",
        linewidth=5,
        color=f"C{i + 2}",
    )
plt.gca().set(
    aspect="equal",
    title="2-dimensional dataset with principal components",
    xlabel="first feature",
    ylabel="second feature",
)
plt.legend()
plt.show()

2-dimensional dataset with principal components

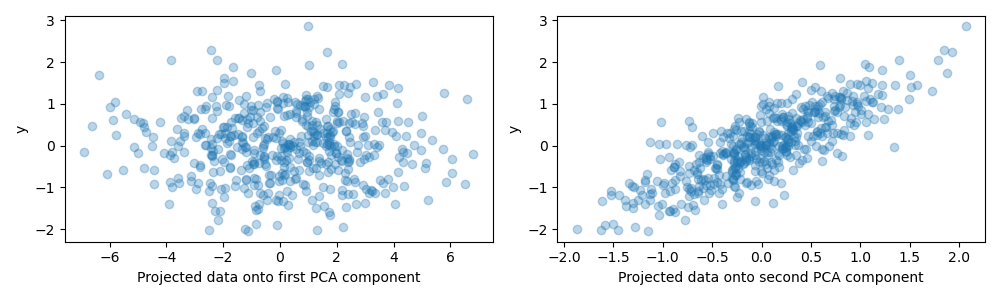
Для целей этого примера мы теперь определяем целевую переменную y таким образом, что она сильно коррелирует с направлением, имеющим малую дисперсию. Для этого мы спроецируем X на второй компонент и добавьте немного шума к нему.

y = X.dot(pca.components_[1]) + rng.normal(size=n_samples) / 2

fig, axes = plt.subplots(1, 2, figsize=(10, 3))

axes[0].scatter(X.dot(pca.components_[0]), y, alpha=0.3)
axes[0].set(xlabel="Projected data onto first PCA component", ylabel="y")
axes[1].scatter(X.dot(pca.components_[1]), y, alpha=0.3)
axes[1].set(xlabel="Projected data onto second PCA component", ylabel="y")
plt.tight_layout()
plt.show()

False: принимает np.inf, np.nan, pd.NA в массиве.#

Теперь мы создаем два регрессора: PCR и PLS, и для наших иллюстративных целей устанавливаем количество компонентов равным 1. Перед подачей данных на шаг PCA в PCR мы сначала стандартизируем их, как рекомендуется хорошей практикой. Оценщик PLS имеет встроенные возможности масштабирования.

Для обеих моделей мы строим проекцию данных на первую компоненту относительно цели. В обоих случаях эти спроецированные данные будут использоваться регрессорами в качестве обучающих данных.

from sklearn.cross_decomposition import PLSRegression
from sklearn.decomposition import PCA
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler

X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=rng)

pcr = make_pipeline(StandardScaler(), PCA(n_components=1), LinearRegression())
pcr.fit(X_train, y_train)
pca = pcr.named_steps["pca"]  # retrieve the PCA step of the pipeline

pls = PLSRegression(n_components=1)
pls.fit(X_train, y_train)

fig, axes = plt.subplots(1, 2, figsize=(10, 3))
axes[0].scatter(pca.transform(X_test), y_test, alpha=0.3, label="ground truth")
axes[0].scatter(
    pca.transform(X_test), pcr.predict(X_test), alpha=0.3, label="predictions"
)
axes[0].set(
    xlabel="Projected data onto first PCA component", ylabel="y", title="PCR / PCA"
)
axes[0].legend()
axes[1].scatter(pls.transform(X_test), y_test, alpha=0.3, label="ground truth")
axes[1].scatter(
    pls.transform(X_test), pls.predict(X_test), alpha=0.3, label="predictions"
)
axes[1].set(xlabel="Projected data onto first PLS component", ylabel="y", title="PLS")
axes[1].legend()
plt.tight_layout()
plt.show()

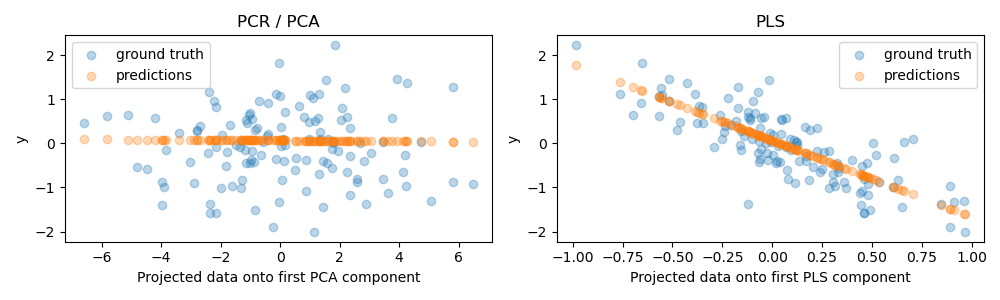
Как и ожидалось, неконтролируемое преобразование PCA в PCR отбросило второй компонент, т.е. направление с наименьшей дисперсией, несмотря на то, что оно является наиболее предсказательным направлением. Это происходит потому, что PCA — полностью неконтролируемое преобразование, и в результате спроецированные данные имеют низкую предсказательную способность для целевой переменной.

С другой стороны, регрессор PLS способен уловить эффект направления с наименьшей дисперсией благодаря использованию информации о цели во время преобразования: он может распознать, что это направление на самом деле является наиболее предсказательным. Отметим, что первый компонент PLS отрицательно коррелирует с целью, что связано с тем, что знаки собственных векторов произвольны.

Мы также выводим R-квадрат обоих оценщиков, что дополнительно подтверждает, что PLS является лучшей альтернативой, чем PCR в этом случае. Отрицательный R-квадрат указывает, что PCR работает хуже, чем регрессор, который просто предсказывает среднее значение целевой переменной.

print(f"PCR r-squared {pcr.score(X_test, y_test):.3f}")
print(f"PLS r-squared {pls.score(X_test, y_test):.3f}")

PCR r-squared -0.026
PLS r-squared 0.658

В заключение отметим, что PCR с 2 компонентами работает так же хорошо, как и PLS: это связано с тем, что в данном случае PCR смог использовать второй компонент, который имеет наибольшую предсказательную силу для цели.

pca_2 = make_pipeline(PCA(n_components=2), LinearRegression())
pca_2.fit(X_train, y_train)
print(f"PCR r-squared with 2 components {pca_2.score(X_test, y_test):.3f}")