Примечание

Перейти в конец чтобы скачать полный пример кода или запустить этот пример в браузере через JupyterLite или Binder.

Параметры SVM с RBF-ядром#

Этот пример иллюстрирует влияние параметров gamma и C радиально-базисной функции (RBF) ядра SVM.

Интуитивно, gamma параметр определяет, насколько далеко распространяется влияние одного обучающего примера, где низкие значения означают 'далеко', а высокие — 'близко'. Параметр gamma параметры можно рассматривать как обратную величину радиуса влияния образцов, выбранных моделью как опорные векторы.

The C параметр балансирует правильную классификацию обучающих примеров против максимизации запаса решающей функции. Для больших значений C, меньший зазор будет принят, если решающая функция лучше классифицирует все обучающие точки правильно. Более низкий C будет способствовать большей марже, следовательно, более простой функции принятия решений, за счёт точности обучения. Другими словами C выступает в качестве параметра регуляризации в SVM.

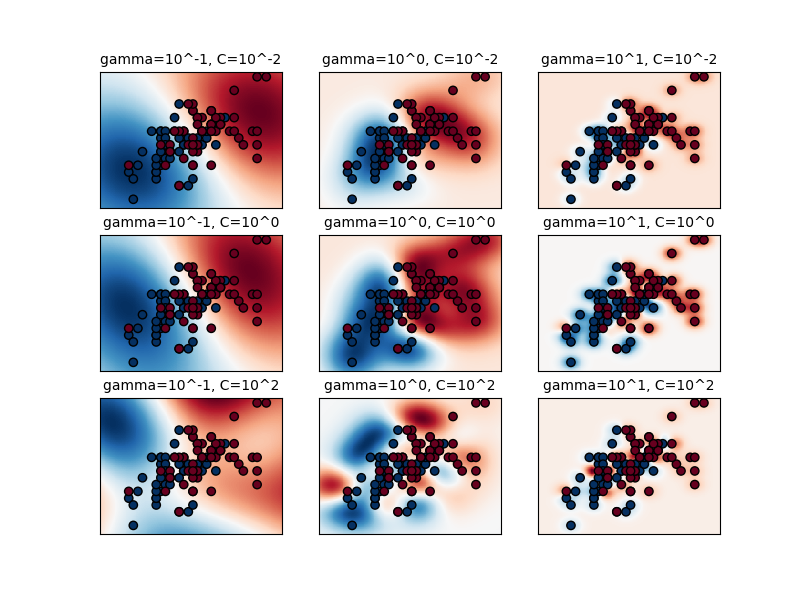
Каждая строка соответствует 8 значениям признаков по порядку. Если

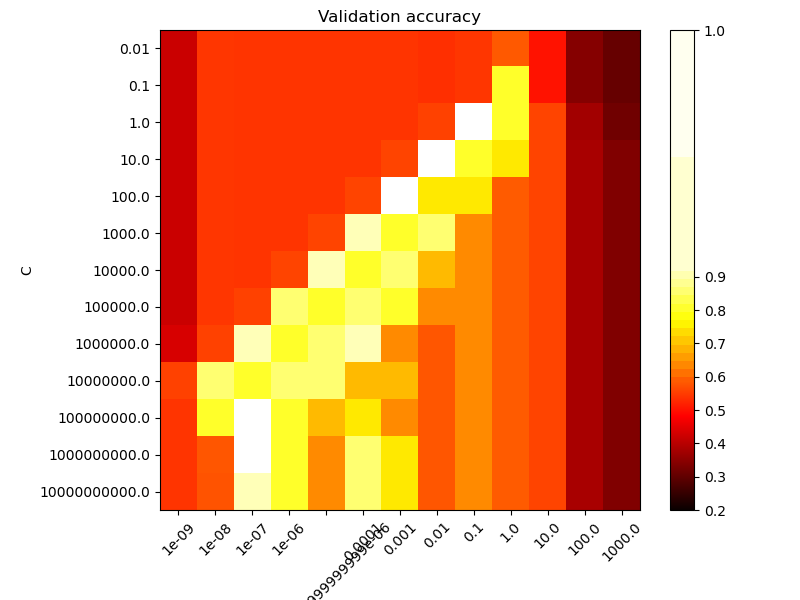
Второй график — это тепловая карта точности перекрестной проверки классификатора как функции C и gamma. Для этого примера мы исследуем относительно большую сетку для иллюстрации. На практике логарифмическая сетка от \(10^{-3}\) to \(10^3\) обычно достаточно. Если лучшие параметры лежат на границах сетки, её можно расширить в этом направлении в последующем поиске.

Обратите внимание, что тепловая карта имеет специальную цветовую шкалу со средним значением, близким к значениям оценки лучших моделей, чтобы их можно было легко различить с первого взгляда.

Поведение модели очень чувствительно к gamma параметр. Если gamma слишком велик, радиус области влияния опорных векторов включает только сам опорный вектор, и никакое количество регуляризации с C сможет предотвратить переобучение.

Когда gamma очень мал, модель слишком ограничена и не может уловить сложность или «форму» данных. Область влияния любого выбранного опорного вектора будет включать весь обучающий набор. Полученная модель будет вести себя аналогично линейной модели с набором гиперплоскостей, разделяющих центры высокой плотности любой пары двух классов.

Для промежуточных значений мы видим на втором графике, что хорошие модели можно найти по диагонали C и gamma. Гладкие модели (нижние gamma значения) могут быть усложнены за счёт увеличения важности правильной классификации каждой точки (большие C значения), отсюда диагональ хорошо работающих моделей.

Наконец, можно также заметить, что для некоторых промежуточных значений gamma мы получаем одинаково работающие модели, когда C становится очень большим. Это говорит о том, что множество опорных векторов больше не меняется. Радиус RBF ядра сам по себе выступает хорошим структурным регуляризатором. Увеличение C дальнейшее не помогает, вероятно, потому что больше нет обучающих точек, нарушающих условия (внутри запаса или неправильно классифицированных), или, по крайней мере, не может быть найдено лучшее решение. При равных оценках может иметь смысл использовать меньший C значения, поскольку очень высокие C значения обычно увеличивают время подгонки.

С другой стороны, более низкие C значения обычно приводят к большему количеству опорных векторов, что может увеличить время предсказания. Поэтому уменьшение значения C предполагает компромисс между временем обучения и временем предсказания.

Мы также должны отметить, что небольшие различия в оценках возникают из-за случайных разбиений процедуры перекрёстной проверки. Эти ложные вариации могут быть сглажены увеличением количества итераций CV n_splits за счет увеличения времени вычислений. Увеличение значения количества C_range и gamma_range шаги увеличат разрешение тепловой карты гиперпараметров.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

Вспомогательный класс для смещения средней точки цветовой карты к значениям, представляющим интерес.

import numpy as np
from matplotlib.colors import Normalize


class MidpointNormalize(Normalize):
    def __init__(self, vmin=None, vmax=None, midpoint=None, clip=False):
        self.midpoint = midpoint
        Normalize.__init__(self, vmin, vmax, clip)

    def __call__(self, value, clip=None):
        x, y = [self.vmin, self.midpoint, self.vmax], [0, 0.5, 1]
        return np.ma.masked_array(np.interp(value, x, y))

Загрузить и подготовить набор данных#

набор данных для поиска по сетке

from sklearn.datasets import load_iris

iris = load_iris()
X = iris.data
y = iris.target

Набор данных для визуализации функции решения: мы сохраняем только первые два признака в X и субдискретизируем набор данных, чтобы оставить только 2 класса и сделать его задачей бинарной классификации.

X_2d = X[:, :2]
X_2d = X_2d[y > 0]
y_2d = y[y > 0]
y_2d -= 1

Обычно рекомендуется масштабировать данные для обучения SVM. В этом примере мы немного обманываем, масштабируя все данные, вместо того чтобы подгонять преобразование на обучающем наборе и просто применять его на тестовом наборе.

from sklearn.preprocessing import StandardScaler

scaler = StandardScaler()
X = scaler.fit_transform(X)
X_2d = scaler.fit_transform(X_2d)

Обучить классификаторы#

Для начального поиска логарифмическая сетка с основанием 10 часто полезна. Используя основание 2, можно достичь более тонкой настройки, но с гораздо большими затратами.

from sklearn.model_selection import GridSearchCV, StratifiedShuffleSplit
from sklearn.svm import SVC

C_range = np.logspace(-2, 10, 13)
gamma_range = np.logspace(-9, 3, 13)
param_grid = dict(gamma=gamma_range, C=C_range)
cv = StratifiedShuffleSplit(n_splits=5, test_size=0.2, random_state=42)
grid = GridSearchCV(SVC(), param_grid=param_grid, cv=cv)
grid.fit(X, y)

print(
    "The best parameters are %s with a score of %0.2f"
    % (grid.best_params_, grid.best_score_)
)

The best parameters are {'C': np.float64(1.0), 'gamma': np.float64(0.1)} with a score of 0.97

Теперь нам нужно обучить классификатор для всех параметров в 2d-версии (мы используем меньший набор параметров здесь, потому что обучение занимает некоторое время)

C_2d_range = [1e-2, 1, 1e2]
gamma_2d_range = [1e-1, 1, 1e1]
classifiers = []
for C in C_2d_range:
    for gamma in gamma_2d_range:
        clf = SVC(C=C, gamma=gamma)
        clf.fit(X_2d, y_2d)
        classifiers.append((C, gamma, clf))

Визуализация#

построить визуализацию эффектов параметров

import matplotlib.pyplot as plt

plt.figure(figsize=(8, 6))
xx, yy = np.meshgrid(np.linspace(-3, 3, 200), np.linspace(-3, 3, 200))
for k, (C, gamma, clf) in enumerate(classifiers):
    # evaluate decision function in a grid
    Z = clf.decision_function(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)

    # visualize decision function for these parameters
    plt.subplot(len(C_2d_range), len(gamma_2d_range), k + 1)
    plt.title("gamma=10^%d, C=10^%d" % (np.log10(gamma), np.log10(C)), size="medium")

    # visualize parameter's effect on decision function
    plt.pcolormesh(xx, yy, -Z, cmap=plt.cm.RdBu)
    plt.scatter(X_2d[:, 0], X_2d[:, 1], c=y_2d, cmap=plt.cm.RdBu_r, edgecolors="k")
    plt.xticks(())
    plt.yticks(())
    plt.axis("tight")

scores = grid.cv_results_["mean_test_score"].reshape(len(C_range), len(gamma_range))

gamma=10^-1, C=10^-2, gamma=10^0, C=10^-2, gamma=10^1, C=10^-2, gamma=10^-1, C=10^0, gamma=10^0, C=10^0, gamma=10^1, C=10^0, gamma=10^-1, C=10^2, gamma=10^0, C=10^2, gamma=10^1, C=10^2

Постройте тепловую карту точности валидации как функции гаммы и C

Оценки кодируются цветами с использованием горячей цветовой карты, которая варьируется от тёмно-красного до ярко-жёлтого. Поскольку наиболее интересные оценки находятся в диапазоне от 0,92 до 0,97, мы используем пользовательский нормализатор, чтобы установить среднюю точку на 0,92, что облегчает визуализацию небольших вариаций значений оценок в интересующем диапазоне, не сводя все низкие значения оценок к одному цвету.

plt.figure(figsize=(8, 6))
plt.subplots_adjust(left=0.2, right=0.95, bottom=0.15, top=0.95)
plt.imshow(
    scores,
    interpolation="nearest",
    cmap=plt.cm.hot,
    norm=MidpointNormalize(vmin=0.2, midpoint=0.92),
)
plt.xlabel("gamma")
plt.ylabel("C")
plt.colorbar()
plt.xticks(np.arange(len(gamma_range)), gamma_range, rotation=45)
plt.yticks(np.arange(len(C_range)), C_range)
plt.title("Validation accuracy")
plt.show()