Примечание

Перейти в конец чтобы скачать полный пример кода или запустить этот пример в браузере через JupyterLite или Binder.

Построение различных классификаторов SVM на наборе данных iris#

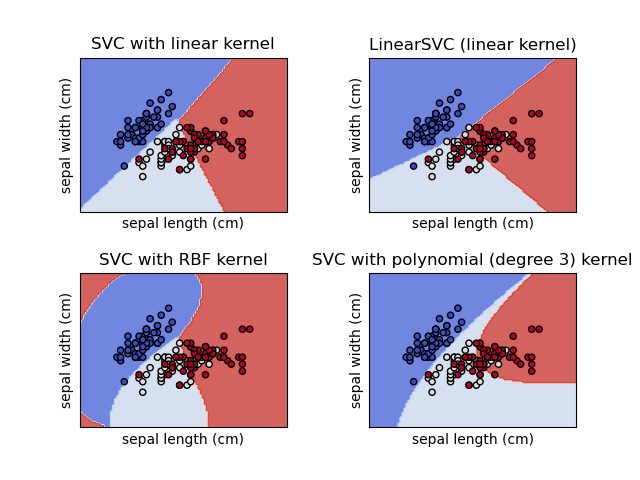
Сравнение различных линейных классификаторов SVM на 2D-проекции набора данных ирисов. Мы рассматриваем только первые 2 признака этого набора данных:

Длина чашелистика
Ширина чашелистика

Этот пример показывает, как построить поверхность решений для четырёх классификаторов SVM с разными ядрами.

Линейные модели LinearSVC() и SVC(kernel='linear') дают слегка разные границы решений. Это может быть следствием следующих различий:

LinearSVC минимизирует квадратичную функцию потерь hinge, SVC минимизирует обычную функцию потерь с шарниром.
LinearSVC использует многоклассовую редукцию One-vs-All (также известную как One-vs-Rest), в то время как SVC использует многоклассовую редукцию One-vs-One.

Обе линейные модели имеют линейные границы решений (пересекающиеся гиперплоскости), в то время как нелинейные модели с ядром (полиномиальные или гауссовские RBF) имеют более гибкие нелинейные границы решений с формами, зависящими от вида ядра и его параметров.

Примечание

Хотя построение функции принятия решений классификаторов для игрушечных 2D наборов данных может помочь получить интуитивное понимание их выразительной способности, имейте в виду, что эти интуиции не всегда обобщаются на более реалистичные многомерные задачи.

SVC with linear kernel, LinearSVC (linear kernel), SVC with RBF kernel, SVC with polynomial (degree 3) kernel

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

import matplotlib.pyplot as plt

from sklearn import datasets, svm
from sklearn.inspection import DecisionBoundaryDisplay

# import some data to play with
iris = datasets.load_iris()
# Take the first two features. We could avoid this by using a two-dim dataset
X = iris.data[:, :2]
y = iris.target

# we create an instance of SVM and fit out data. We do not scale our
# data since we want to plot the support vectors
C = 1.0  # SVM regularization parameter
models = (
    svm.SVC(kernel="linear", C=C),
    svm.LinearSVC(C=C, max_iter=10000),
    svm.SVC(kernel="rbf", gamma=0.7, C=C),
    svm.SVC(kernel="poly", degree=3, gamma="auto", C=C),
)
models = (clf.fit(X, y) for clf in models)

# title for the plots
titles = (
    "SVC with linear kernel",
    "LinearSVC (linear kernel)",
    "SVC with RBF kernel",
    "SVC with polynomial (degree 3) kernel",
)

# Set-up 2x2 grid for plotting.
fig, sub = plt.subplots(2, 2)
plt.subplots_adjust(wspace=0.4, hspace=0.4)

X0, X1 = X[:, 0], X[:, 1]

for clf, title, ax in zip(models, titles, sub.flatten()):
    disp = DecisionBoundaryDisplay.from_estimator(
        clf,
        X,
        response_method="predict",
        cmap=plt.cm.coolwarm,
        alpha=0.8,
        ax=ax,
        xlabel=iris.feature_names[0],
        ylabel=iris.feature_names[1],
    )
    ax.scatter(X0, X1, c=y, cmap=plt.cm.coolwarm, s=20, edgecolors="k")
    ax.set_xticks(())
    ax.set_yticks(())
    ax.set_title(title)

plt.show()