Примечание
Перейти в конец чтобы скачать полный пример кода или запустить этот пример в браузере через JupyterLite или Binder.
Масштабирование параметра регуляризации для SVC#
Следующий пример иллюстрирует эффект масштабирования параметра регуляризации при использовании Метод опорных векторов для классификация. Для классификации SVC нас интересует минимизация риска для уравнения:
где
\(C\) используется для установки количества регуляризации
\(\mathcal{L}\) является
lossфункция наших образцов и параметров нашей модели.\(\Omega\) является
penaltyфункция параметров нашей модели
Если мы рассматриваем функцию потерь как индивидуальную ошибку на выборку, то термин соответствия данным, или сумма ошибок для каждой выборки, увеличивается по мере добавления большего количества выборок. Однако штрафной член не увеличивается.
При использовании, например, кросс-валидация, чтобы задать
количество регуляризации с Cмежду основной задачей и меньшими задачами внутри фолдов кросс-валидации будет разное количество образцов.
Поскольку функция потерь зависит от количества выборок, последнее влияет на выбранное значение C. Возникает вопрос: "Как оптимально настроить C, чтобы учесть разное количество обучающих выборок?"
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
Генерация данных#
В этом примере мы исследуем эффект перепараметризации параметра регуляризации C для учета количества образцов при использовании либо L1, либо L2
штрафа. Для этой цели мы создаем синтетический набор данных с большим количеством
признаков, из которых лишь немногие являются информативными. Поэтому мы ожидаем, что
регуляризация сожмет коэффициенты к нулю (штраф L2) или точно
к нулю (штраф L1).
from sklearn.datasets import make_classification
n_samples, n_features = 100, 300
X, y = make_classification(
n_samples=n_samples, n_features=n_features, n_informative=5, random_state=1
)
случай L1-штрафа#
В случае L1 теория говорит, что при сильной регуляризации оценщик не может предсказывать так же хорошо, как модель, знающая истинное распределение (даже в пределе, когда размер выборки стремится к бесконечности), поскольку он может установить некоторые веса предсказательных признаков в ноль, что вызывает смещение. Однако она говорит, что можно найти правильный набор ненулевых параметров, а также их знаки, настраивая C.
Мы определяем линейный SVC с L1-штрафом.
Мы вычисляем средний тестовый балл для различных значений C с помощью перекрестной проверки.
import numpy as np
import pandas as pd
from sklearn.model_selection import ShuffleSplit, validation_curve
Cs = np.logspace(-2.3, -1.3, 10)
train_sizes = np.linspace(0.3, 0.7, 3)
labels = [f"fraction: {train_size}" for train_size in train_sizes]
shuffle_params = {
"test_size": 0.3,
"n_splits": 150,
"random_state": 1,
}
results = {"C": Cs}
for label, train_size in zip(labels, train_sizes):
cv = ShuffleSplit(train_size=train_size, **shuffle_params)
train_scores, test_scores = validation_curve(
model_l1,
X,
y,
param_name="C",
param_range=Cs,
cv=cv,
n_jobs=2,
)
results[label] = test_scores.mean(axis=1)
results = pd.DataFrame(results)
import matplotlib.pyplot as plt
fig, axes = plt.subplots(nrows=1, ncols=2, sharey=True, figsize=(12, 6))
# plot results without scaling C
results.plot(x="C", ax=axes[0], logx=True)
axes[0].set_ylabel("CV score")
axes[0].set_title("No scaling")
for label in labels:
best_C = results.loc[results[label].idxmax(), "C"]
axes[0].axvline(x=best_C, linestyle="--", color="grey", alpha=0.7)
# plot results by scaling C
for train_size_idx, label in enumerate(labels):
train_size = train_sizes[train_size_idx]
results_scaled = results[[label]].assign(
C_scaled=Cs * float(n_samples * np.sqrt(train_size))
)
results_scaled.plot(x="C_scaled", ax=axes[1], logx=True, label=label)
best_C_scaled = results_scaled["C_scaled"].loc[results[label].idxmax()]
axes[1].axvline(x=best_C_scaled, linestyle="--", color="grey", alpha=0.7)
axes[1].set_title("Scaling C by sqrt(1 / n_samples)")
_ = fig.suptitle("Effect of scaling C with L1 penalty")
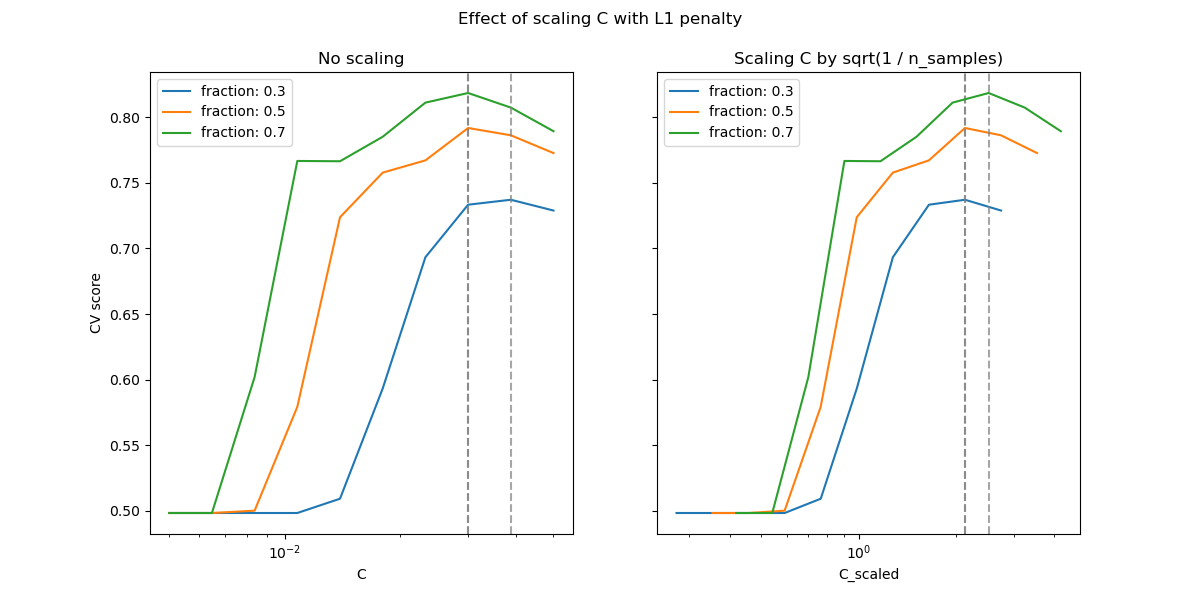
В области малых C (сильная регуляризация) все коэффициенты, изученные моделями, равны нулю, что приводит к сильному недообучению. Действительно, точность в этой области находится на уровне случайного угадывания.
Использование масштаба по умолчанию даёт довольно стабильное оптимальное значение C,
тогда как переход из области недообучения зависит от количества
обучающих образцов. Перепараметризация приводит к еще более стабильным результатам.
Обратите внимание, что при всех этих стратегиях О предсказательной производительности Lasso или Одновременный анализ Lasso и селектора Данцига где параметр регуляризации всегда предполагается пропорциональным 1 / sqrt(n_samples).
случай L2-штрафа#
Мы можем провести аналогичный эксперимент с L2-штрафом. В этом случае теория говорит, что для достижения согласованности прогнозирования параметр штрафа должен оставаться постоянным по мере роста количества выборок.
model_l2 = LinearSVC(penalty="l2", loss="squared_hinge", dual=True)
Cs = np.logspace(-8, 4, 11)
labels = [f"fraction: {train_size}" for train_size in train_sizes]
results = {"C": Cs}
for label, train_size in zip(labels, train_sizes):
cv = ShuffleSplit(train_size=train_size, **shuffle_params)
train_scores, test_scores = validation_curve(
model_l2,
X,
y,
param_name="C",
param_range=Cs,
cv=cv,
n_jobs=2,
)
results[label] = test_scores.mean(axis=1)
results = pd.DataFrame(results)
import matplotlib.pyplot as plt
fig, axes = plt.subplots(nrows=1, ncols=2, sharey=True, figsize=(12, 6))
# plot results without scaling C
results.plot(x="C", ax=axes[0], logx=True)
axes[0].set_ylabel("CV score")
axes[0].set_title("No scaling")
for label in labels:
best_C = results.loc[results[label].idxmax(), "C"]
axes[0].axvline(x=best_C, linestyle="--", color="grey", alpha=0.8)
# plot results by scaling C
for train_size_idx, label in enumerate(labels):
results_scaled = results[[label]].assign(
C_scaled=Cs * float(n_samples * np.sqrt(train_sizes[train_size_idx]))
)
results_scaled.plot(x="C_scaled", ax=axes[1], logx=True, label=label)
best_C_scaled = results_scaled["C_scaled"].loc[results[label].idxmax()]
axes[1].axvline(x=best_C_scaled, linestyle="--", color="grey", alpha=0.8)
axes[1].set_title("Scaling C by sqrt(1 / n_samples)")
fig.suptitle("Effect of scaling C with L2 penalty")
plt.show()
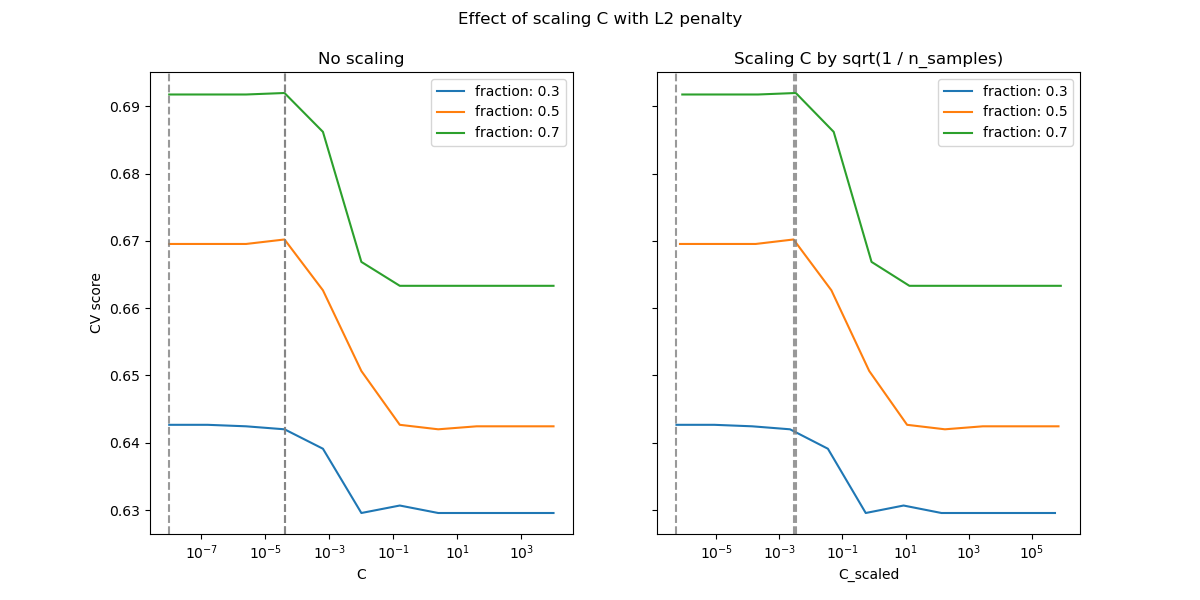
Для случая штрафа L2 перепараметризация, по-видимому, оказывает меньшее влияние на стабильность оптимального значения регуляризации. Переход из области переобучения происходит в более широком диапазоне, и точность, по-видимому, не ухудшается до уровня случайности.
Попробуйте увеличить значение до n_splits=1_000 для лучших результатов в случае L2,
что не показано здесь из-за ограничений сборщика документации.
Общее время выполнения скрипта: (0 минут 18.718 секунд)
Связанные примеры
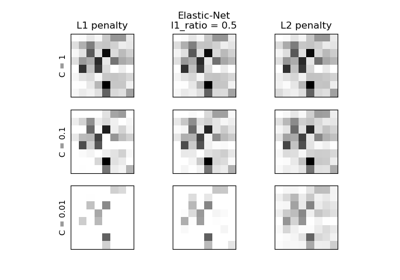
L1-штраф и разреженность в логистической регрессии

Влияние регуляризации модели на ошибку обучения и тестирования