Примечание
Перейти в конец чтобы скачать полный пример кода или запустить этот пример в браузере через JupyterLite или Binder.
Использование KBinsDiscretizer для дискретизации непрерывных признаков#
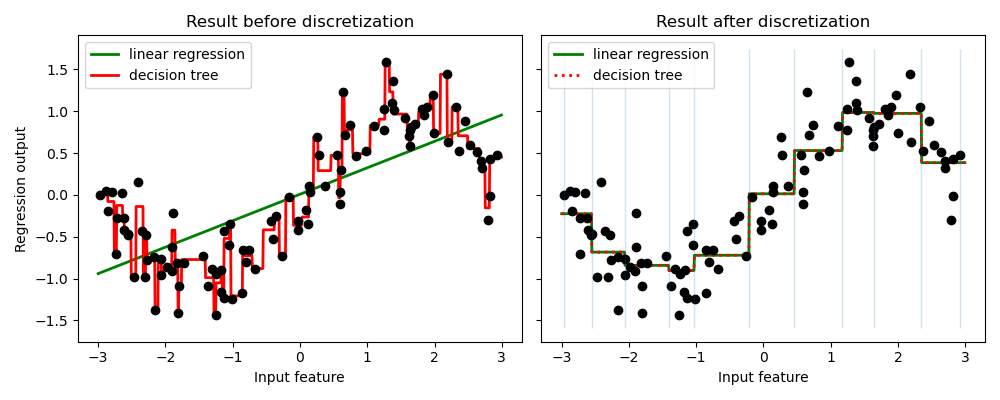
Пример сравнивает результат прогнозирования линейной регрессии (линейная модель) и дерева решений (модель на основе дерева) с дискретизацией и без дискретизации вещественных признаков.
Как показано в результате до дискретизации, линейная модель строится быстро и относительно проста для интерпретации, но может моделировать только линейные зависимости, в то время как дерево решений может построить гораздо более сложную модель данных. Один из способов сделать линейную модель более мощной для непрерывных данных — использовать дискретизацию (также известную как бининг). В примере мы дискретизируем признак и выполняем one-hot кодирование преобразованных данных. Обратите внимание, что если интервалы недостаточно широки, может существенно возрасти риск переобучения, поэтому параметры дискретизатора обычно следует настраивать с помощью кросс-валидации.
После дискретизации линейная регрессия и дерево решений делают точно такой же прогноз. Поскольку признаки постоянны в пределах каждого бина, любая модель должна предсказывать одно и то же значение для всех точек в бине. По сравнению с результатом до дискретизации, линейная модель становится гораздо более гибкой, а дерево решений становится гораздо менее гибким. Обратите внимание, что бининг признаков обычно не оказывает полезного эффекта для моделей на основе деревьев, так как эти модели могут научиться разделять данные в любом месте.
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
import matplotlib.pyplot as plt
import numpy as np
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import KBinsDiscretizer
from sklearn.tree import DecisionTreeRegressor
# construct the dataset
rnd = np.random.RandomState(42)
X = rnd.uniform(-3, 3, size=100)
y = np.sin(X) + rnd.normal(size=len(X)) / 3
X = X.reshape(-1, 1)
# transform the dataset with KBinsDiscretizer
enc = KBinsDiscretizer(
n_bins=10, encode="onehot", quantile_method="averaged_inverted_cdf"
)
X_binned = enc.fit_transform(X)
# predict with original dataset
fig, (ax1, ax2) = plt.subplots(ncols=2, sharey=True, figsize=(10, 4))
line = np.linspace(-3, 3, 1000, endpoint=False).reshape(-1, 1)
reg = LinearRegression().fit(X, y)
ax1.plot(line, reg.predict(line), linewidth=2, color="green", label="linear regression")
reg = DecisionTreeRegressor(min_samples_split=3, random_state=0).fit(X, y)
ax1.plot(line, reg.predict(line), linewidth=2, color="red", label="decision tree")
ax1.plot(X[:, 0], y, "o", c="k")
ax1.legend(loc="best")
ax1.set_ylabel("Regression output")
ax1.set_xlabel("Input feature")
ax1.set_title("Result before discretization")
# predict with transformed dataset
line_binned = enc.transform(line)
reg = LinearRegression().fit(X_binned, y)
ax2.plot(
line,
reg.predict(line_binned),
linewidth=2,
color="green",
linestyle="-",
label="linear regression",
)
reg = DecisionTreeRegressor(min_samples_split=3, random_state=0).fit(X_binned, y)
ax2.plot(
line,
reg.predict(line_binned),
linewidth=2,
color="red",
linestyle=":",
label="decision tree",
)
ax2.plot(X[:, 0], y, "o", c="k")
ax2.vlines(enc.bin_edges_[0], *plt.gca().get_ylim(), linewidth=1, alpha=0.2)
ax2.legend(loc="best")
ax2.set_xlabel("Input feature")
ax2.set_title("Result after discretization")
plt.tight_layout()
plt.show()
Общее время выполнения скрипта: (0 минут 0.183 секунды)
Связанные примеры
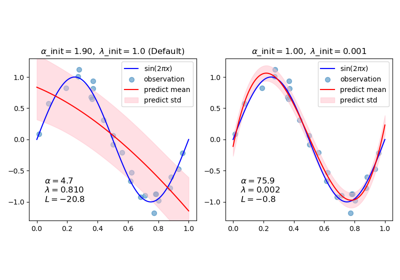
Аппроксимация кривой с использованием байесовской гребневой регрессии