Примечание
Перейти в конец чтобы скачать полный пример кода или запустить этот пример в браузере через JupyterLite или Binder.
Сравнить методы перекрёстного разложения#
Простое использование различных алгоритмов перекрестного разложения:
PLSCanonical
PLSRegression, с многомерным откликом, также известный как PLS2
PLSRegression, с одномерным откликом, также известный как PLS1
CCA
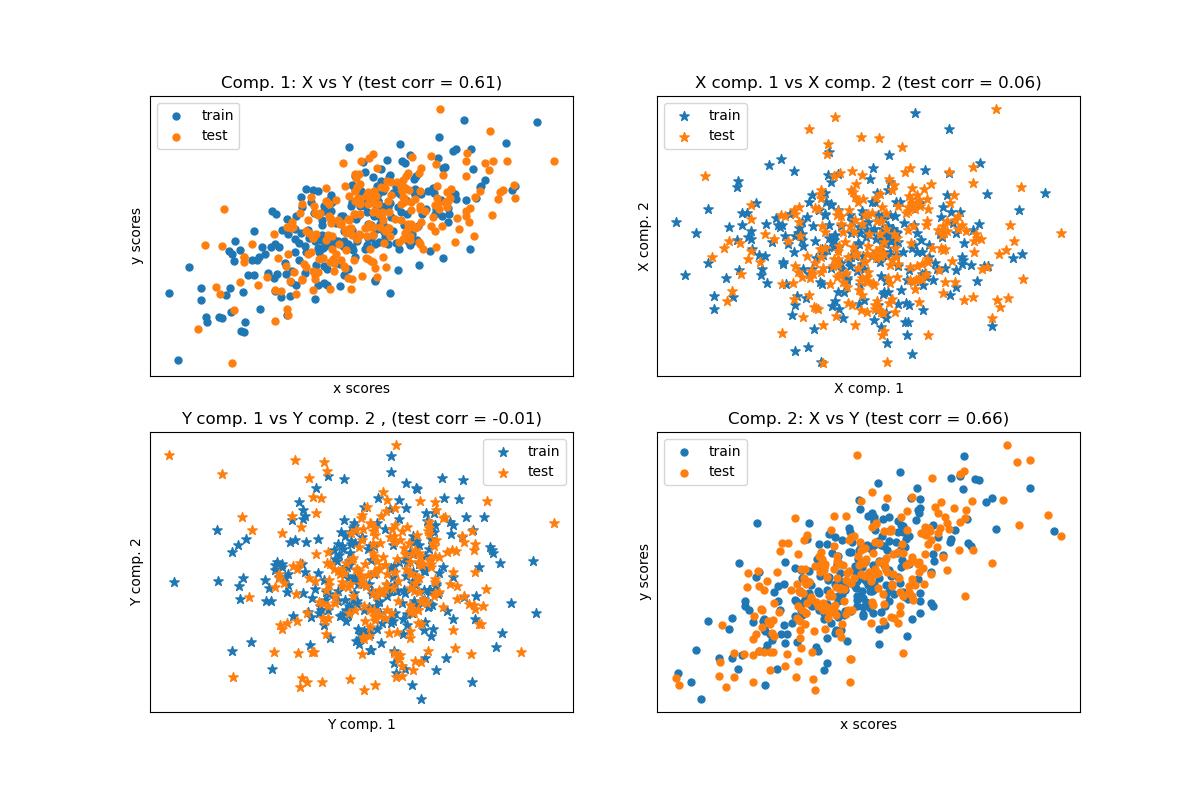
Для двух многомерных коварирующих двумерных наборов данных, X и Y, PLS извлекает 'направления ковариации', т.е. компоненты каждого набора данных, которые объясняют наибольшую общую дисперсию между обоими наборами данных. Это видно на матрица диаграмм рассеяния отображение: компоненты 1 в наборе данных X и наборе данных Y максимально коррелированы (точки лежат вокруг первой диагонали). Это также верно для компонентов 2 в обоих наборах данных, однако корреляция между наборами данных для разных компонентов слаба: облако точек очень сферическое.
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
Модель латентных переменных на основе набора данных#
import numpy as np
from sklearn.model_selection import train_test_split
rng = np.random.default_rng(42)
n = 500
# 2 latents vars:
l1 = rng.normal(size=n)
l2 = rng.normal(size=n)
latents = np.array([l1, l1, l2, l2]).T
X = latents + rng.normal(size=(n, 4))
Y = latents + rng.normal(size=(n, 4))
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.5, shuffle=False)
print("Corr(X)")
print(np.round(np.corrcoef(X.T), 2))
print("Corr(Y)")
print(np.round(np.corrcoef(Y.T), 2))
Corr(X)
[[ 1. 0.48 -0.01 0. ]
[ 0.48 1. -0.01 0. ]
[-0.01 -0.01 1. 0.49]
[ 0. 0. 0.49 1. ]]
Corr(Y)
[[ 1. 0.47 0.03 0.05]
[ 0.47 1. 0.03 -0.01]
[ 0.03 0.03 1. 0.5 ]
[ 0.05 -0.01 0.5 1. ]]
Канонический (симметричный) PLS#
Преобразование данных#
from sklearn.cross_decomposition import PLSCanonical
plsca = PLSCanonical(n_components=2)
plsca.fit(X_train, Y_train)
X_train_r, Y_train_r = plsca.transform(X_train, Y_train)
X_test_r, Y_test_r = plsca.transform(X_test, Y_test)
Диаграмма рассеяния оценок#
import matplotlib.pyplot as plt
# On diagonal plot X vs Y scores on each components
plt.figure(figsize=(12, 8))
plt.subplot(221)
plt.scatter(X_train_r[:, 0], Y_train_r[:, 0], label="train", marker="o", s=25)
plt.scatter(X_test_r[:, 0], Y_test_r[:, 0], label="test", marker="o", s=25)
plt.xlabel("x scores")
plt.ylabel("y scores")
plt.title(
"Comp. 1: X vs Y (test corr = %.2f)"
% np.corrcoef(X_test_r[:, 0], Y_test_r[:, 0])[0, 1]
)
plt.xticks(())
plt.yticks(())
plt.legend(loc="best")
plt.subplot(224)
plt.scatter(X_train_r[:, 1], Y_train_r[:, 1], label="train", marker="o", s=25)
plt.scatter(X_test_r[:, 1], Y_test_r[:, 1], label="test", marker="o", s=25)
plt.xlabel("x scores")
plt.ylabel("y scores")
plt.title(
"Comp. 2: X vs Y (test corr = %.2f)"
% np.corrcoef(X_test_r[:, 1], Y_test_r[:, 1])[0, 1]
)
plt.xticks(())
plt.yticks(())
plt.legend(loc="best")
# Off diagonal plot components 1 vs 2 for X and Y
plt.subplot(222)
plt.scatter(X_train_r[:, 0], X_train_r[:, 1], label="train", marker="*", s=50)
plt.scatter(X_test_r[:, 0], X_test_r[:, 1], label="test", marker="*", s=50)
plt.xlabel("X comp. 1")
plt.ylabel("X comp. 2")
plt.title(
"X comp. 1 vs X comp. 2 (test corr = %.2f)"
% np.corrcoef(X_test_r[:, 0], X_test_r[:, 1])[0, 1]
)
plt.legend(loc="best")
plt.xticks(())
plt.yticks(())
plt.subplot(223)
plt.scatter(Y_train_r[:, 0], Y_train_r[:, 1], label="train", marker="*", s=50)
plt.scatter(Y_test_r[:, 0], Y_test_r[:, 1], label="test", marker="*", s=50)
plt.xlabel("Y comp. 1")
plt.ylabel("Y comp. 2")
plt.title(
"Y comp. 1 vs Y comp. 2 , (test corr = %.2f)"
% np.corrcoef(Y_test_r[:, 0], Y_test_r[:, 1])[0, 1]
)
plt.legend(loc="best")
plt.xticks(())
plt.yticks(())
plt.show()
PLS-регрессия с многомерным откликом, также известная как PLS2#
from sklearn.cross_decomposition import PLSRegression
n = 1000
q = 3
p = 10
X = rng.normal(size=(n, p))
B = np.array([[1, 2] + [0] * (p - 2)] * q).T
# each Yj = 1*X1 + 2*X2 + noize
Y = np.dot(X, B) + rng.normal(size=(n, q)) + 5
pls2 = PLSRegression(n_components=3)
pls2.fit(X, Y)
print("True B (such that: Y = XB + Err)")
print(B)
# compare pls2.coef_ with B
print("Estimated B")
print(np.round(pls2.coef_, 1))
pls2.predict(X)
True B (such that: Y = XB + Err)
[[1 1 1]
[2 2 2]
[0 0 0]
[0 0 0]
[0 0 0]
[0 0 0]
[0 0 0]
[0 0 0]
[0 0 0]
[0 0 0]]
Estimated B
[[ 1. 2. 0. -0. 0. 0. 0. 0. 0. -0. ]
[ 1. 2. 0. -0. -0. -0. -0. -0.1 -0. 0. ]
[ 1. 2. 0. -0. 0. 0. -0. -0. 0. 0. ]]
array([[4.09928294, 4.27252412, 4.116446 ],
[3.22383315, 3.36186659, 3.2829478 ],
[6.40665836, 6.45699286, 6.28414926],
...,
[1.50716084, 1.50460976, 1.5177967 ],
[6.67188307, 6.51139993, 6.47838503],
[5.93803911, 5.99272896, 5.91191611]], shape=(1000, 3))
PLS-регрессия, с одномерным откликом, также известная как PLS1#
n = 1000
p = 10
X = rng.normal(size=(n, p))
y = X[:, 0] + 2 * X[:, 1] + rng.normal(size=n) + 5
pls1 = PLSRegression(n_components=3)
pls1.fit(X, y)
# note that the number of components exceeds 1 (the dimension of y)
print("Estimated betas")
print(np.round(pls1.coef_, 1))
Estimated betas
[[ 1. 2. -0. 0. -0. 0. -0.1 0. -0. -0. ]]
CCA (режим PLS B с симметричной дефляцией)#
Общее время выполнения скрипта: (0 минут 0.162 секунды)
Связанные примеры
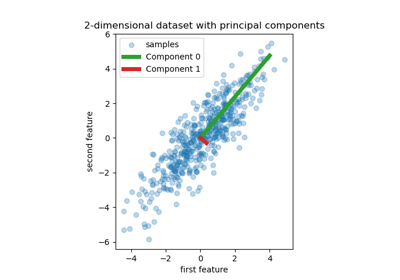
Регрессия на главных компонентах против регрессии методом частичных наименьших квадратов
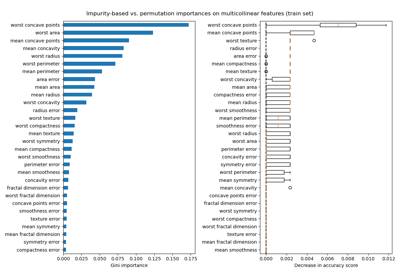
Важность перестановок с мультиколлинеарными или коррелированными признаками