Примечание
Перейти в конец чтобы скачать полный пример кода или запустить этот пример в браузере через JupyterLite или Binder.
Сравнение алгоритмов обнаружения аномалий для выявления выбросов на игрушечных наборах данных#
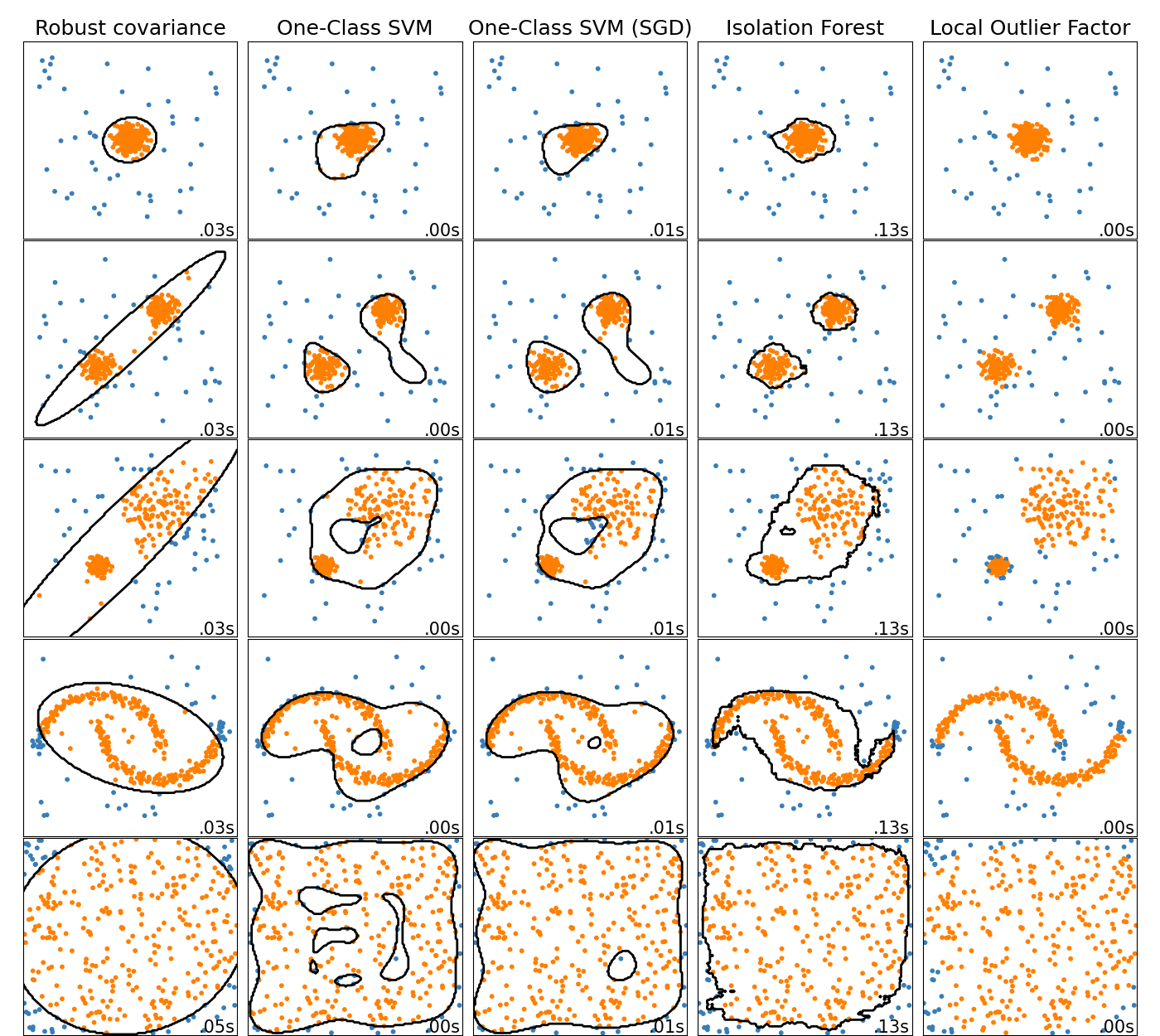
Этот пример показывает характеристики различных алгоритмов обнаружения аномалий на 2D наборах данных. Наборы данных содержат одну или две моды (области высокой плотности) для иллюстрации способности алгоритмов справляться с мультимодальными данными.
Для каждого набора данных 15% образцов генерируются как случайный равномерный шум. Эта доля — значение, заданное параметру nu OneClassSVM и параметру contamination других алгоритмов обнаружения выбросов. Границы решений между нормальными точками и выбросами отображаются черным цветом, за исключением Local Outlier Factor (LOF), так как у него нет метода predict для применения на новых данных при использовании для обнаружения выбросов.
The OneClassSVM известен своей чувствительностью к выбросам и
поэтому не очень хорошо подходит для обнаружения аномалий. Этот оценщик лучше всего
подходит для обнаружения новизны, когда обучающая выборка не загрязнена
выбросами. Тем не менее, обнаружение выбросов в высоких размерностях или без каких-либо
предположений о распределении нормальных данных является очень сложной задачей, и
одноклассовый SVM может дать полезные результаты в этих ситуациях в зависимости от
значения его гиперпараметров.
The sklearn.linear_model.SGDOneClassSVM является реализацией
One-Class SVM на основе стохастического градиентного спуска (SGD). В сочетании с аппроксимацией ядра
этот оценщик может использоваться для приближенного решения
ядерного sklearn.svm.OneClassSVM. Отметим, что, хотя и не идентичны, границы решений
sklearn.linear_model.SGDOneClassSVM и те из
sklearn.svm.OneClassSVM очень похожи. Основное преимущество использования
sklearn.linear_model.SGDOneClassSVM заключается в том, что он масштабируется линейно с количеством образцов.
sklearn.covariance.EllipticEnvelope предполагает, что данные распределены по Гауссу, и
обучает эллипс. Таким образом, он ухудшается, когда данные не унимодальны. Однако обратите внимание,
что этот оценщик устойчив к выбросам.
IsolationForest и
LocalOutlierFactor кажутся достаточно хорошо работающими
для многомодальных наборов данных. Преимущество
LocalOutlierFactor над другими оценщиками
показан для третьего набора данных, где два режима имеют разную плотность.
Это преимущество объясняется локальным аспектом LOF, означающим, что он только
сравнивает оценку аномальности одного образца с оценками его соседей.
Наконец, для последнего набора данных трудно сказать, что один образец более аномален, чем другой, поскольку они равномерно распределены в гиперкубе. За исключением OneClassSVM который немного переобучается, все оценщики представляют достойные решения для этой ситуации. В таком случае было бы разумно внимательнее посмотреть на оценки аномальности образцов, так как хороший оценщик должен присваивать схожие оценки всем образцам.
Хотя эти примеры дают некоторое представление об алгоритмах, это представление может не применяться к данным очень высокой размерности.
Наконец, обратите внимание, что параметры моделей здесь были подобраны вручную, но на практике их нужно настраивать. При отсутствии размеченных данных проблема полностью неконтролируема, поэтому выбор модели может быть сложной задачей.
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
import time
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
from sklearn import svm
from sklearn.covariance import EllipticEnvelope
from sklearn.datasets import make_blobs, make_moons
from sklearn.ensemble import IsolationForest
from sklearn.kernel_approximation import Nystroem
from sklearn.linear_model import SGDOneClassSVM
from sklearn.neighbors import LocalOutlierFactor
from sklearn.pipeline import make_pipeline
matplotlib.rcParams["contour.negative_linestyle"] = "solid"
# Example settings
n_samples = 300
outliers_fraction = 0.15
n_outliers = int(outliers_fraction * n_samples)
n_inliers = n_samples - n_outliers
# define outlier/anomaly detection methods to be compared.
# the SGDOneClassSVM must be used in a pipeline with a kernel approximation
# to give similar results to the OneClassSVM
anomaly_algorithms = [
(
"Robust covariance",
EllipticEnvelope(contamination=outliers_fraction, random_state=42),
),
("One-Class SVM", svm.OneClassSVM(nu=outliers_fraction, kernel="rbf", gamma=0.1)),
(
"One-Class SVM (SGD)",
make_pipeline(
Nystroem(gamma=0.1, random_state=42, n_components=150),
SGDOneClassSVM(
nu=outliers_fraction,
shuffle=True,
fit_intercept=True,
random_state=42,
tol=1e-6,
),
),
),
(
"Isolation Forest",
IsolationForest(contamination=outliers_fraction, random_state=42),
),
(
"Local Outlier Factor",
LocalOutlierFactor(n_neighbors=35, contamination=outliers_fraction),
),
]
# Define datasets
blobs_params = dict(random_state=0, n_samples=n_inliers, n_features=2)
datasets = [
make_blobs(centers=[[0, 0], [0, 0]], cluster_std=0.5, **blobs_params)[0],
make_blobs(centers=[[2, 2], [-2, -2]], cluster_std=[0.5, 0.5], **blobs_params)[0],
make_blobs(centers=[[2, 2], [-2, -2]], cluster_std=[1.5, 0.3], **blobs_params)[0],
4.0
* (
make_moons(n_samples=n_samples, noise=0.05, random_state=0)[0]
- np.array([0.5, 0.25])
),
14.0 * (np.random.RandomState(42).rand(n_samples, 2) - 0.5),
]
# Compare given classifiers under given settings
xx, yy = np.meshgrid(np.linspace(-7, 7, 150), np.linspace(-7, 7, 150))
plt.figure(figsize=(len(anomaly_algorithms) * 2 + 4, 12.5))
plt.subplots_adjust(
left=0.02, right=0.98, bottom=0.001, top=0.96, wspace=0.05, hspace=0.01
)
plot_num = 1
rng = np.random.RandomState(42)
for i_dataset, X in enumerate(datasets):
# Add outliers
X = np.concatenate([X, rng.uniform(low=-6, high=6, size=(n_outliers, 2))], axis=0)
for name, algorithm in anomaly_algorithms:
t0 = time.time()
algorithm.fit(X)
t1 = time.time()
plt.subplot(len(datasets), len(anomaly_algorithms), plot_num)
if i_dataset == 0:
plt.title(name, size=18)
# fit the data and tag outliers
if name == "Local Outlier Factor":
y_pred = algorithm.fit_predict(X)
else:
y_pred = algorithm.fit(X).predict(X)
# plot the levels lines and the points
if name != "Local Outlier Factor": # LOF does not implement predict
Z = algorithm.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
plt.contour(xx, yy, Z, levels=[0], linewidths=2, colors="black")
colors = np.array(["#377eb8", "#ff7f00"])
plt.scatter(X[:, 0], X[:, 1], s=10, color=colors[(y_pred + 1) // 2])
plt.xlim(-7, 7)
plt.ylim(-7, 7)
plt.xticks(())
plt.yticks(())
plt.text(
0.99,
0.01,
("%.2fs" % (t1 - t0)).lstrip("0"),
transform=plt.gca().transAxes,
size=15,
horizontalalignment="right",
)
plot_num += 1
plt.show()
Общее время выполнения скрипта: (0 минут 3.279 секунд)
Связанные примеры
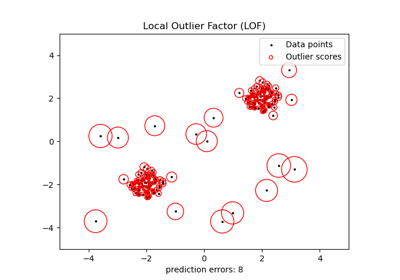
Обнаружение выбросов с помощью фактора локальных выбросов (LOF)

Обнаружение новизны с помощью локального фактора выбросов (LOF)
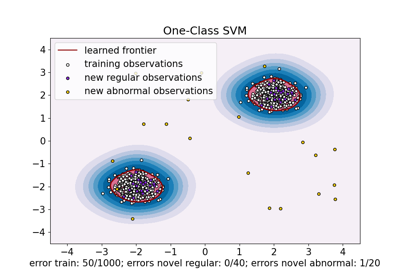
One-Class SVM против One-Class SVM с использованием стохастического градиентного спуска