Примечание
Перейти в конец чтобы скачать полный пример кода или запустить этот пример в браузере через JupyterLite или Binder.
Построение кривых обучения и проверка масштабируемости моделей#
В этом примере мы покажем, как использовать класс
LearningCurveDisplay для легкого построения кривых обучения. Кроме того, мы даем интерпретацию полученным кривым обучения для наивного байесовского и SVM классификаторов.
Затем мы исследуем и делаем выводы о масштабируемости этих прогнозных моделей, рассматривая их вычислительную стоимость, а не только их статистическую точность.
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
Кривая обучения#
Кривые обучения показывают эффект добавления большего количества выборок во время процесса обучения. Эффект изображается путем проверки статистической производительности модели в терминах оценки обучения и оценки тестирования.
Здесь мы вычисляем кривую обучения наивного байесовского классификатора и классификатора SVM с ядром RBF, используя набор данных digits.
from sklearn.datasets import load_digits
from sklearn.naive_bayes import GaussianNB
from sklearn.svm import SVC
X, y = load_digits(return_X_y=True)
naive_bayes = GaussianNB()
svc = SVC(kernel="rbf", gamma=0.001)
The from_estimator
отображает кривую обучения для данного набора данных и прогнозной модели для анализа. Чтобы получить оценку неопределённости оценок, этот метод использует процедуру перекрёстной проверки.
import matplotlib.pyplot as plt
import numpy as np
from sklearn.model_selection import LearningCurveDisplay, ShuffleSplit
fig, ax = plt.subplots(nrows=1, ncols=2, figsize=(10, 6), sharey=True)
common_params = {
"X": X,
"y": y,
"train_sizes": np.linspace(0.1, 1.0, 5),
"cv": ShuffleSplit(n_splits=50, test_size=0.2, random_state=0),
"score_type": "both",
"n_jobs": 4,
"line_kw": {"marker": "o"},
"std_display_style": "fill_between",
"score_name": "Accuracy",
}
for ax_idx, estimator in enumerate([naive_bayes, svc]):
LearningCurveDisplay.from_estimator(estimator, **common_params, ax=ax[ax_idx])
handles, label = ax[ax_idx].get_legend_handles_labels()
ax[ax_idx].legend(handles[:2], ["Training Score", "Test Score"])
ax[ax_idx].set_title(f"Learning Curve for {estimator.__class__.__name__}")
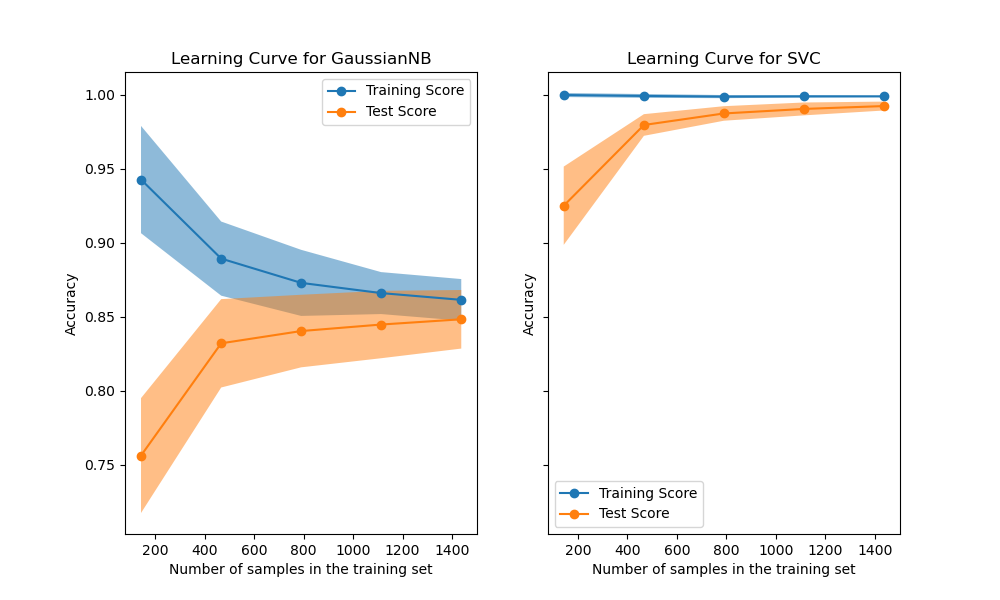
Сначала мы анализируем кривую обучения наивного байесовского классификатора. Её форма часто встречается в более сложных наборах данных: оценка обучения очень высока при использовании небольшого количества выборок для обучения и уменьшается при увеличении количества выборок, тогда как тестовая оценка изначально низка, а затем увеличивается при добавлении выборок. Оценки обучения и тестирования становятся более реалистичными, когда все выборки используются для обучения.
Мы видим еще одну типичную кривую обучения для классификатора SVM с ядром RBF. Оценка на обучении остается высокой независимо от размера обучающей выборки. С другой стороны, оценка на тесте увеличивается с размером обучающей выборки. Действительно, она увеличивается до точки, где достигает плато. Наблюдение такого плато указывает на то, что может быть нецелесообразно собирать новые данные для обучения модели, поскольку обобщающая способность модели больше не будет увеличиваться.
Анализ сложности#
В дополнение к этим кривым обучения также можно рассмотреть масштабируемость прогностических моделей с точки зрения времени обучения и оценки.
The LearningCurveDisplay класс не
предоставляет такую информацию. Нам нужно прибегнуть к
learning_curve функцию вместо этого и создать
график вручную.
from sklearn.model_selection import learning_curve
common_params = {
"X": X,
"y": y,
"train_sizes": np.linspace(0.1, 1.0, 5),
"cv": ShuffleSplit(n_splits=50, test_size=0.2, random_state=0),
"n_jobs": 4,
"return_times": True,
}
train_sizes, _, test_scores_nb, fit_times_nb, score_times_nb = learning_curve(
naive_bayes, **common_params
)
train_sizes, _, test_scores_svm, fit_times_svm, score_times_svm = learning_curve(
svc, **common_params
)
fig, ax = plt.subplots(nrows=2, ncols=2, figsize=(16, 12), sharex=True)
for ax_idx, (fit_times, score_times, estimator) in enumerate(
zip(
[fit_times_nb, fit_times_svm],
[score_times_nb, score_times_svm],
[naive_bayes, svc],
)
):
# scalability regarding the fit time
ax[0, ax_idx].plot(train_sizes, fit_times.mean(axis=1), "o-")
ax[0, ax_idx].fill_between(
train_sizes,
fit_times.mean(axis=1) - fit_times.std(axis=1),
fit_times.mean(axis=1) + fit_times.std(axis=1),
alpha=0.3,
)
ax[0, ax_idx].set_ylabel("Fit time (s)")
ax[0, ax_idx].set_title(
f"Scalability of the {estimator.__class__.__name__} classifier"
)
# scalability regarding the score time
ax[1, ax_idx].plot(train_sizes, score_times.mean(axis=1), "o-")
ax[1, ax_idx].fill_between(
train_sizes,
score_times.mean(axis=1) - score_times.std(axis=1),
score_times.mean(axis=1) + score_times.std(axis=1),
alpha=0.3,
)
ax[1, ax_idx].set_ylabel("Score time (s)")
ax[1, ax_idx].set_xlabel("Number of training samples")
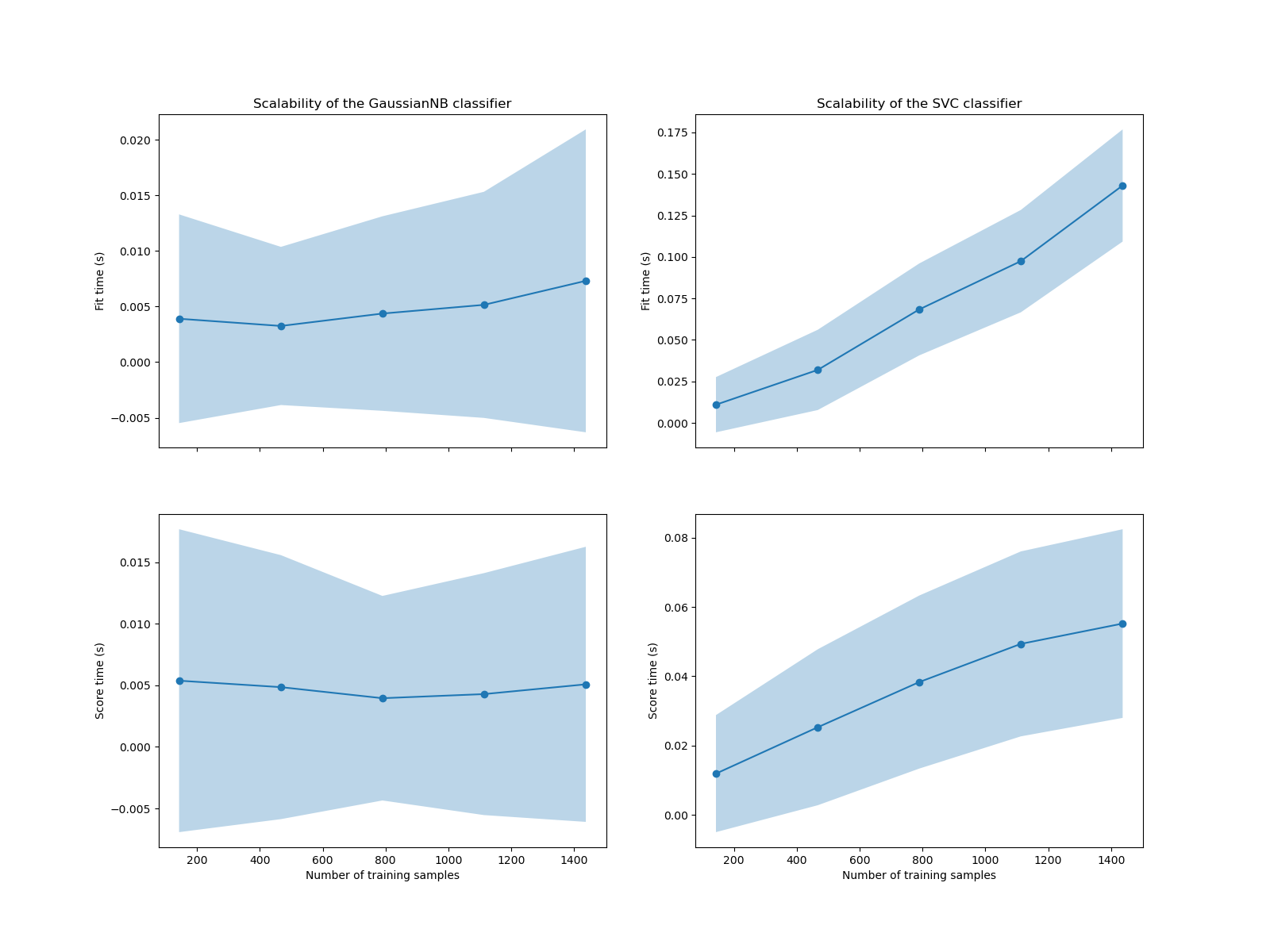
Мы видим, что масштабируемость классификаторов SVM и наивного Байеса очень разная. Сложность классификатора SVM при обучении и оценке быстро растёт с увеличением количества выборок. Действительно, известно, что временная сложность обучения этого классификатора более чем квадратична относительно количества выборок, что затрудняет масштабирование на наборах данных с более чем несколькими десятками тысяч выборок. В отличие от этого, классификатор наивного Байеса масштабируется гораздо лучше с более низкой сложностью при обучении и оценке.
Впоследствии мы можем проверить компромисс между увеличением времени обучения и оценкой перекрестной проверки.
fig, ax = plt.subplots(nrows=1, ncols=2, figsize=(16, 6))
for ax_idx, (fit_times, test_scores, estimator) in enumerate(
zip(
[fit_times_nb, fit_times_svm],
[test_scores_nb, test_scores_svm],
[naive_bayes, svc],
)
):
ax[ax_idx].plot(fit_times.mean(axis=1), test_scores.mean(axis=1), "o-")
ax[ax_idx].fill_between(
fit_times.mean(axis=1),
test_scores.mean(axis=1) - test_scores.std(axis=1),
test_scores.mean(axis=1) + test_scores.std(axis=1),
alpha=0.3,
)
ax[ax_idx].set_ylabel("Accuracy")
ax[ax_idx].set_xlabel("Fit time (s)")
ax[ax_idx].set_title(
f"Performance of the {estimator.__class__.__name__} classifier"
)
plt.show()
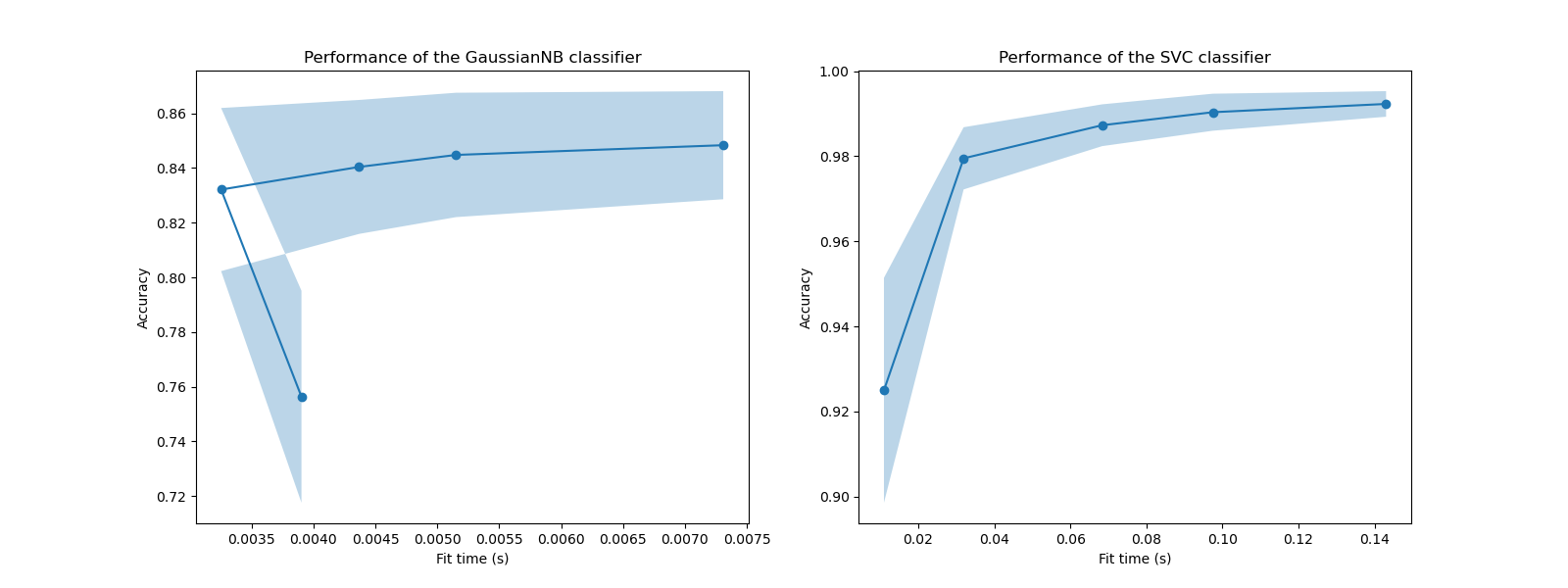
На этих графиках мы можем искать точку перегиба, после которой оценка перекрестной проверки больше не увеличивается, а увеличивается только время обучения.
Общее время выполнения скрипта: (0 минут 32.877 секунд)
Связанные примеры
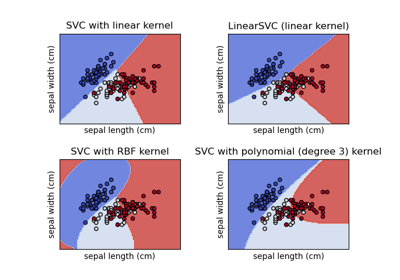
Построение различных классификаторов SVM на наборе данных iris