Примечание
Перейти в конец чтобы скачать полный пример кода или запустить этот пример в браузере через JupyterLite или Binder.
Неспособность машинного обучения выводить причинно-следственные связи#
Модели машинного обучения отлично подходят для измерения статистических ассоциаций. К сожалению, если мы не готовы делать сильные предположения о данных, эти модели не могут выводить причинно-следственные эффекты.
Чтобы проиллюстрировать это, мы смоделируем ситуацию, в которой пытаемся ответить на один из самых важных вопросов в экономике образования: каков причинный эффект получения высшего образования на почасовую оплату? Хотя ответ на этот вопрос имеет решающее значение для политиков, Смещения из-за пропущенных переменных (OVB) мешает нам идентифицировать этот причинный эффект.
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
Набор данных: смоделированные почасовые зарплаты#
Процесс генерации данных описан в коде ниже. Опыт работы в годах и мера способностей извлекаются из нормальных распределений; почасовая оплата одного из родителей извлекается из бета-распределения. Затем мы создаём индикатор наличия высшего образования, на который положительно влияют способности и почасовая оплата родителей. Наконец, мы моделируем почасовую оплату как линейную функцию всех предыдущих переменных и случайной составляющей. Обратите внимание, что все переменные положительно влияют на почасовую оплату.
import numpy as np
import pandas as pd
n_samples = 10_000
rng = np.random.RandomState(32)
experiences = rng.normal(20, 10, size=n_samples).astype(int)
experiences[experiences < 0] = 0
abilities = rng.normal(0, 0.15, size=n_samples)
parent_hourly_wages = 50 * rng.beta(2, 8, size=n_samples)
parent_hourly_wages[parent_hourly_wages < 0] = 0
college_degrees = (
9 * abilities + 0.02 * parent_hourly_wages + rng.randn(n_samples) > 0.7
).astype(int)
true_coef = pd.Series(
{
"college degree": 2.0,
"ability": 5.0,
"experience": 0.2,
"parent hourly wage": 1.0,
}
)
hourly_wages = (
true_coef["experience"] * experiences
+ true_coef["parent hourly wage"] * parent_hourly_wages
+ true_coef["college degree"] * college_degrees
+ true_coef["ability"] * abilities
+ rng.normal(0, 1, size=n_samples)
)
hourly_wages[hourly_wages < 0] = 0
Описание смоделированных данных#
Поскольку шум по-прежнему нормально распределен, в частности симметричен, истинное условное среднее и истинная условная медиана совпадают. Действительно, мы видим, что оцененная медиана почти достигает истинного среднего. Мы наблюдаем эффект увеличения дисперсии шума на 5% и 95% квантили: наклоны этих квантилей сильно различаются, и интервал между ними становится шире с увеличением
import seaborn as sns
df = pd.DataFrame(
{
"college degree": college_degrees,
"ability": abilities,
"hourly wage": hourly_wages,
"experience": experiences,
"parent hourly wage": parent_hourly_wages,
}
)
grid = sns.pairplot(df, diag_kind="kde", corner=True)
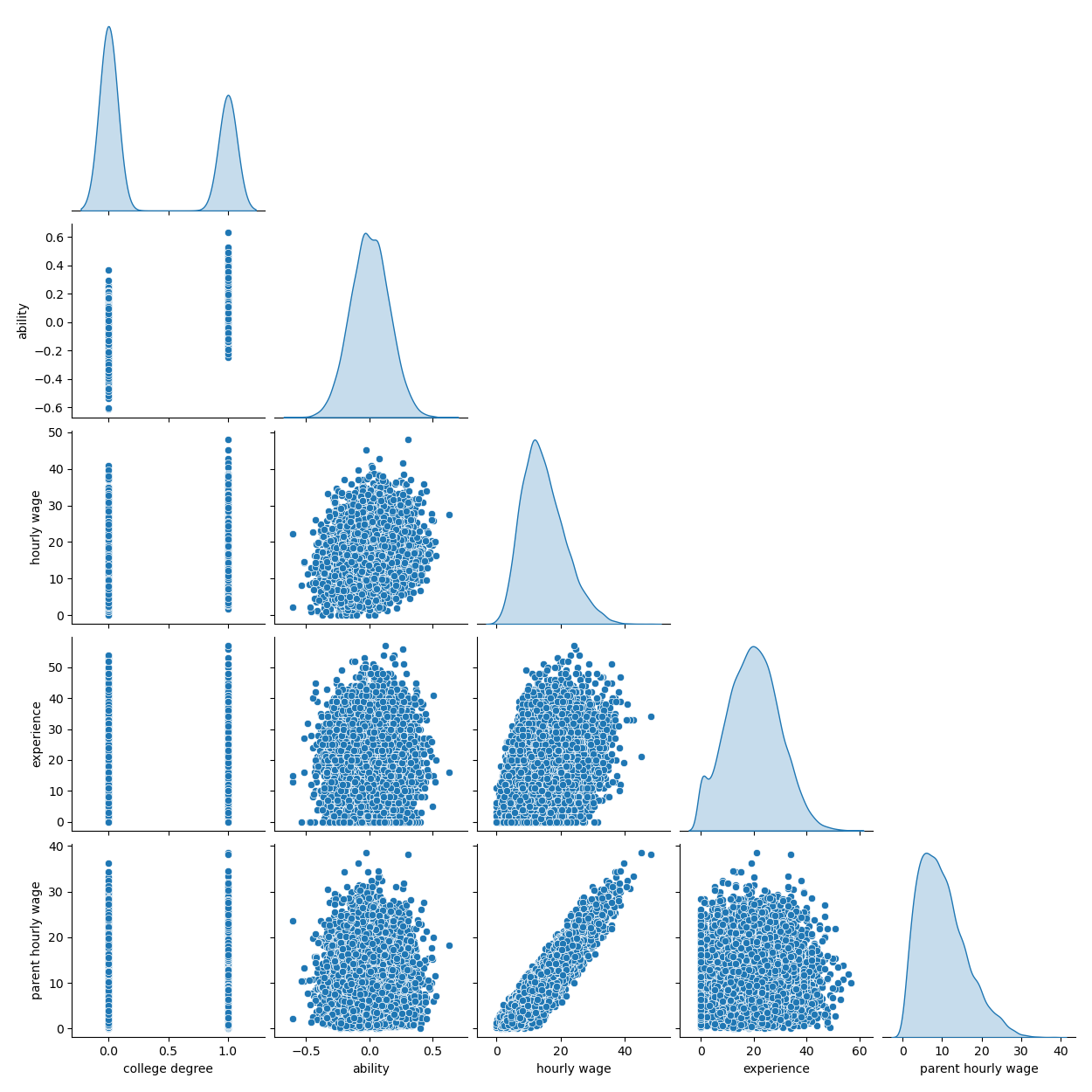
В следующем разделе мы обучаем прогнозные модели и поэтому отделяем целевой столбец от признаков, а также разделяем данные на обучающую и тестовую выборки.
from sklearn.model_selection import train_test_split
target_name = "hourly wage"
X, y = df.drop(columns=target_name), df[target_name]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)
Прогнозирование дохода с полностью наблюдаемыми переменными#
Сначала мы обучаем прогнозную модель,
LinearRegression модели. В этом эксперименте
мы предполагаем, что все переменные, используемые истинной генеративной моделью, доступны.
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score
features_names = ["experience", "parent hourly wage", "college degree", "ability"]
regressor_with_ability = LinearRegression()
regressor_with_ability.fit(X_train[features_names], y_train)
y_pred_with_ability = regressor_with_ability.predict(X_test[features_names])
R2_with_ability = r2_score(y_test, y_pred_with_ability)
print(f"R2 score with ability: {R2_with_ability:.3f}")
R2 score with ability: 0.975
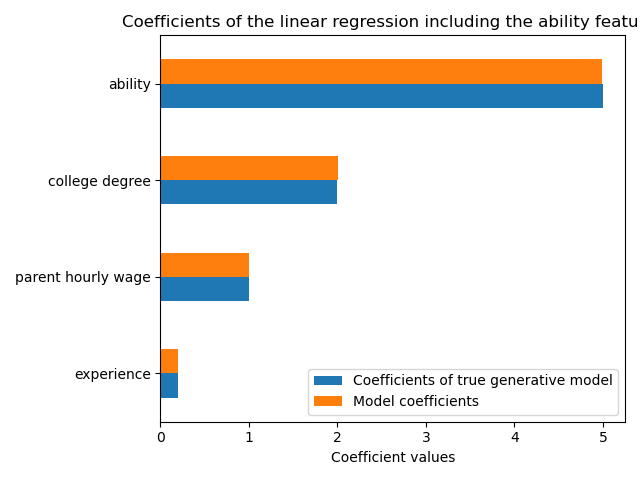
Эта модель хорошо предсказывает почасовую заработную плату, как показано высоким показателем R2. Мы строим график коэффициентов модели, чтобы показать, что мы точно восстанавливаем значения истинной генеративной модели.
import matplotlib.pyplot as plt
model_coef = pd.Series(regressor_with_ability.coef_, index=features_names)
coef = pd.concat(
[true_coef[features_names], model_coef],
keys=["Coefficients of true generative model", "Model coefficients"],
axis=1,
)
ax = coef.plot.barh()
ax.set_xlabel("Coefficient values")
ax.set_title("Coefficients of the linear regression including the ability features")
_ = plt.tight_layout()
Прогнозирование дохода с частичными наблюдениями#
На практике интеллектуальные способности не наблюдаются или оцениваются только по прокси-переменным, которые непреднамеренно измеряют также образование (например, с помощью тестов IQ). Но исключение признака "способности" из линейной модели завышает оценку через положительное смещение от пропущенных переменных.
features_names = ["experience", "parent hourly wage", "college degree"]
regressor_without_ability = LinearRegression()
regressor_without_ability.fit(X_train[features_names], y_train)
y_pred_without_ability = regressor_without_ability.predict(X_test[features_names])
R2_without_ability = r2_score(y_test, y_pred_without_ability)
print(f"R2 score without ability: {R2_without_ability:.3f}")
R2 score without ability: 0.968
Прогностическая способность нашей модели аналогична, когда мы опускаем признак способности с точки зрения оценки R2. Теперь мы проверяем, отличаются ли коэффициенты модели от истинной генеративной модели.
model_coef = pd.Series(regressor_without_ability.coef_, index=features_names)
coef = pd.concat(
[true_coef[features_names], model_coef],
keys=["Coefficients of true generative model", "Model coefficients"],
axis=1,
)
ax = coef.plot.barh()
ax.set_xlabel("Coefficient values")
_ = ax.set_title("Coefficients of the linear regression excluding the ability feature")
plt.tight_layout()
plt.show()
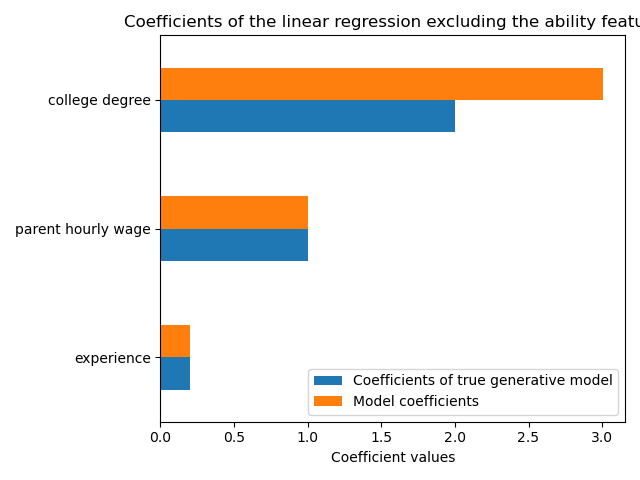
Чтобы компенсировать пропущенную переменную, модель завышает коэффициент признака высшего образования. Поэтому интерпретация этого значения коэффициента как причинного эффекта истинной генеративной модели неверна.
Извлеченные уроки#
Модели машинного обучения не предназначены для оценки причинных эффектов. Хотя мы показали это с линейной моделью, OVB может повлиять на любой тип модели.
При интерпретации коэффициента или изменения предсказаний, вызванного изменением одного из признаков, важно учитывать потенциально ненаблюдаемые переменные, которые могут коррелировать как с рассматриваемым признаком, так и с целевой переменной. Такие переменные называются Смешивающие переменные. Чтобы всё ещё оценивать причинный эффект при наличии смешивающих факторов, исследователи обычно проводят эксперименты, в которых переменная лечения (например, высшее образование) рандомизирована. Когда эксперимент слишком дорог или неэтичен, исследователи иногда могут использовать другие методы причинного вывода, такие как Инструментальные переменные (IV) оценки.
Общее время выполнения скрипта: (0 минут 1.928 секунд)
Связанные примеры

Распространённые ошибки в интерпретации коэффициентов линейных моделей
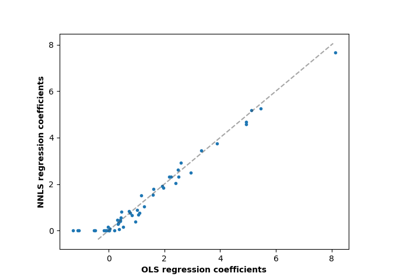
Метод наименьших квадратов с неотрицательными ограничениями

Влияние регуляризации модели на ошибку обучения и тестирования