Примечание

Перейти в конец чтобы скачать полный пример кода или запустить этот пример в браузере через JupyterLite или Binder.

Недообучение vs. Переобучение#

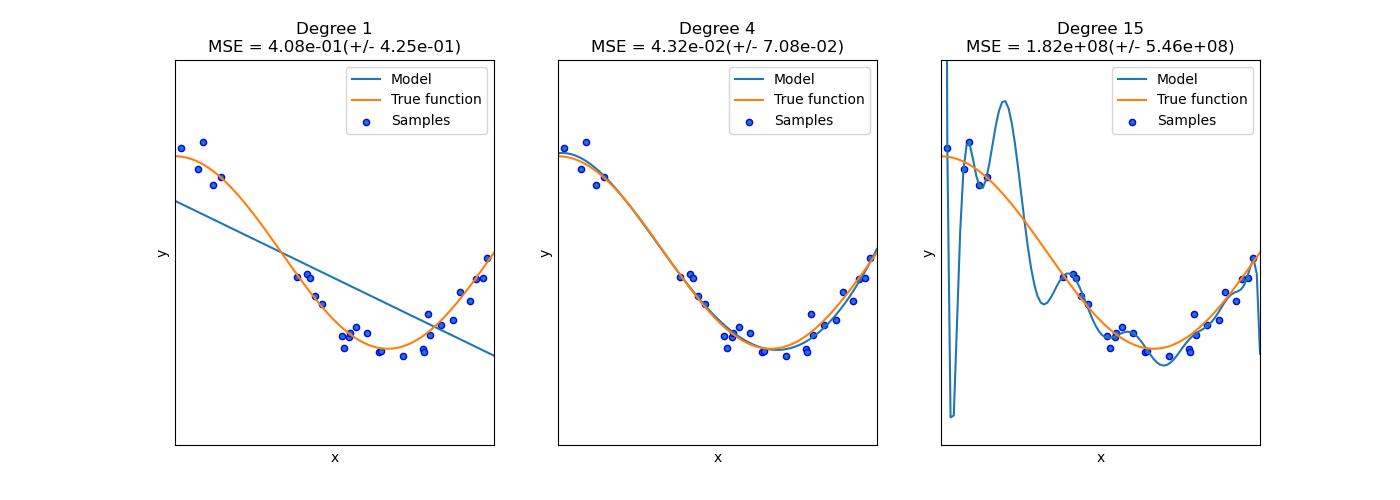
Этот пример демонстрирует проблемы недообучения и переобучения и как мы можем использовать линейную регрессию с полиномиальными признаками для аппроксимации нелинейных функций. График показывает функцию, которую мы хотим аппроксимировать, являющуюся частью функции косинуса. Кроме того, отображаются выборки из реальной функции и аппроксимации различных моделей. Модели имеют полиномиальные признаки разной степени. Мы видим, что линейная функция (полином степени 1) недостаточна для подгонки обучающих выборок. Это называется недообучение. Полином степени 4 приближает истинную функцию почти идеально. Однако для более высоких степеней модель будет переобучение обучающие данные, т.е. он изучает шум обучающих данных. Мы оцениваем количественно переобучение / недообучение с использованием кросс-валидации. Мы вычисляем среднеквадратичную ошибку (MSE) на валидационной выборке: чем выше, тем менее вероятно, что модель корректно обобщает данные из обучающей выборки.

Degree 1 MSE = 4.08e-01(+/- 4.25e-01), Degree 4 MSE = 4.32e-02(+/- 7.08e-02), Degree 15 MSE = 1.82e+08(+/- 5.46e+08)

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

import matplotlib.pyplot as plt
import numpy as np

from sklearn.linear_model import LinearRegression
from sklearn.model_selection import cross_val_score
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures


def true_fun(X):
    return np.cos(1.5 * np.pi * X)


np.random.seed(0)

n_samples = 30
degrees = [1, 4, 15]

X = np.sort(np.random.rand(n_samples))
y = true_fun(X) + np.random.randn(n_samples) * 0.1

plt.figure(figsize=(14, 5))
for i in range(len(degrees)):
    ax = plt.subplot(1, len(degrees), i + 1)
    plt.setp(ax, xticks=(), yticks=())

    polynomial_features = PolynomialFeatures(degree=degrees[i], include_bias=False)
    linear_regression = LinearRegression()
    pipeline = Pipeline(
        [
            ("polynomial_features", polynomial_features),
            ("linear_regression", linear_regression),
        ]
    )
    pipeline.fit(X[:, np.newaxis], y)

    # Evaluate the models using crossvalidation
    scores = cross_val_score(
        pipeline, X[:, np.newaxis], y, scoring="neg_mean_squared_error", cv=10
    )

    X_test = np.linspace(0, 1, 100)
    plt.plot(X_test, pipeline.predict(X_test[:, np.newaxis]), label="Model")
    plt.plot(X_test, true_fun(X_test), label="True function")
    plt.scatter(X, y, edgecolor="b", s=20, label="Samples")
    plt.xlabel("x")
    plt.ylabel("y")
    plt.xlim((0, 1))
    plt.ylim((-2, 2))
    plt.legend(loc="best")
    plt.title(
        "Degree {}\nMSE = {:.2e}(+/- {:.2e})".format(
            degrees[i], -scores.mean(), scores.std()
        )
    )
plt.show()