Примечание
Перейти в конец чтобы скачать полный пример кода или запустить этот пример в браузере через JupyterLite или Binder.
Лаггированные признаки для прогнозирования временных рядов#
Этот пример демонстрирует, как созданные с помощью Polars лаговые признаки могут быть использованы
для прогнозирования временных рядов с
HistGradientBoostingRegressor на наборе данных Bike Sharing Demand.
См. пример на Инженерия временных признаков для некоторого исследования данных на этом наборе данных и демонстрации периодического конструирования признаков.
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
Анализ набора данных о спросе на прокат велосипедов#
Мы начинаем с загрузки данных из репозитория OpenML в виде необработанного файла parquet, чтобы проиллюстрировать работу с произвольным файлом parquet вместо того, чтобы скрывать этот шаг в удобном инструменте, таком как sklearn.datasets.fetch_openml.
URL файла parquet можно найти в JSON-описании набора данных Bike Sharing Demand с id 44063 на openml.org (https://openml.org/search?type=data&status=active&id=44063).
The sha256 хэш файла также предоставляется для обеспечения целостности
загруженного файла.
import numpy as np
import polars as pl
from sklearn.datasets import fetch_file
pl.Config.set_fmt_str_lengths(20)
bike_sharing_data_file = fetch_file(
"https://data.openml.org/datasets/0004/44063/dataset_44063.pq",
sha256="d120af76829af0d256338dc6dd4be5df4fd1f35bf3a283cab66a51c1c6abd06a",
)
bike_sharing_data_file
PosixPath('/home/circleci/scikit_learn_data/data.openml.org/datasets_0004_44063/dataset_44063.pq')
Мы загружаем файл parquet с помощью Polars для разработки признаков. Polars автоматически кэширует общие подвыражения, которые повторно используются в нескольких выражениях (как pl.col("count").shift(1) ниже). См.
https://docs.pola.rs/user-guide/lazy/optimizations/ для получения дополнительной информации.
df = pl.read_parquet(bike_sharing_data_file)
Далее мы рассмотрим статистическую сводку набора данных, чтобы лучше понять данные, с которыми работаем.
import polars.selectors as cs
summary = df.select(cs.numeric()).describe()
summary
Давайте посмотрим на количество сезонов "fall", "spring", "summer"
и "winter" присутствующих в наборе данных, чтобы убедиться, что они сбалансированы.
import matplotlib.pyplot as plt
df["season"].value_counts()
Генерация лаговых признаков с использованием Polars#
Рассмотрим задачу прогнозирования спроса на следующий час по данным о прошлом спросе. Поскольку спрос — это непрерывная переменная, интуитивно можно использовать любую модель регрессии. Однако у нас нет обычного (X_train, y_train) набор данных. Вместо этого у нас просто есть
y_train требуют данных, организованных последовательно по времени.
lagged_df = df.select(
"count",
*[pl.col("count").shift(i).alias(f"lagged_count_{i}h") for i in [1, 2, 3]],
lagged_count_1d=pl.col("count").shift(24),
lagged_count_1d_1h=pl.col("count").shift(24 + 1),
lagged_count_7d=pl.col("count").shift(7 * 24),
lagged_count_7d_1h=pl.col("count").shift(7 * 24 + 1),
lagged_mean_24h=pl.col("count").shift(1).rolling_mean(24),
lagged_max_24h=pl.col("count").shift(1).rolling_max(24),
lagged_min_24h=pl.col("count").shift(1).rolling_min(24),
lagged_mean_7d=pl.col("count").shift(1).rolling_mean(7 * 24),
lagged_max_7d=pl.col("count").shift(1).rolling_max(7 * 24),
lagged_min_7d=pl.col("count").shift(1).rolling_min(7 * 24),
)
lagged_df.tail(10)
Однако будьте осторожны, первые строки имеют неопределенные значения, потому что их собственное прошлое неизвестно. Это зависит от того, сколько лага мы использовали:
lagged_df.head(10)
Теперь мы можем разделить лаговые признаки в матрице X и целевая переменная (количества для предсказания) в массиве той же первой размерности y.
lagged_df = lagged_df.drop_nulls()
X = lagged_df.drop("count")
y = lagged_df["count"]
print("X shape: {}\ny shape: {}".format(X.shape, y.shape))
X shape: (17210, 13)
y shape: (17210,)
Наивная оценка регрессии спроса на велосипеды на следующий час#
Давайте случайным образом разделим наш табличный набор данных для обучения модели градиентного бустинга регрессионных деревьев (GBRT) и оценим её с использованием средней абсолютной процентной ошибки (MAPE). Если наша модель предназначена для прогнозирования (т.е. предсказания будущих данных на основе прошлых данных), мы не должны использовать обучающие данные, которые позже тестовых данных. В машинном обучении временных рядов предположение «i.i.d» (независимые и одинаково распределённые) не выполняется, так как точки данных не являются независимыми и имеют временную связь.
from sklearn.ensemble import HistGradientBoostingRegressor
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.2, random_state=42
)
model = HistGradientBoostingRegressor().fit(X_train, y_train)
Взглянув на производительность модели.
from sklearn.metrics import mean_absolute_percentage_error
y_pred = model.predict(X_test)
mean_absolute_percentage_error(y_test, y_pred)
0.3889873516666431
Правильная оценка прогнозирования на следующий час#
Давайте используем правильную стратегию разделения для оценки, которая учитывает временную структуру набора данных, чтобы оценить способность нашей модели предсказывать точки данных в будущем (чтобы избежать жульничества путем чтения значений из лаговых признаков в обучающем наборе).
from sklearn.model_selection import TimeSeriesSplit
ts_cv = TimeSeriesSplit(
n_splits=3, # to keep the notebook fast enough on common laptops
gap=48, # 2 days data gap between train and test
max_train_size=10000, # keep train sets of comparable sizes
test_size=3000, # for 2 or 3 digits of precision in scores
)
all_splits = list(ts_cv.split(X, y))
Обучение модели и оценка её производительности на основе MAPE.
train_idx, test_idx = all_splits[0]
X_train, X_test = X[train_idx, :], X[test_idx, :]
y_train, y_test = y[train_idx], y[test_idx]
model = HistGradientBoostingRegressor().fit(X_train, y_train)
y_pred = model.predict(X_test)
mean_absolute_percentage_error(y_test, y_pred)
0.44300751539296973
Ошибка обобщения, измеренная через перемешанное разделение на обучающую и тестовую выборки, слишком оптимистична. Обобщение через временное разделение, вероятно, более репрезентативно для истинной производительности модели регрессии. Давайте оценим эту изменчивость нашей оценки ошибки с помощью правильной кросс-валидации:
from sklearn.model_selection import cross_val_score
cv_mape_scores = -cross_val_score(
model, X, y, cv=ts_cv, scoring="neg_mean_absolute_percentage_error"
)
cv_mape_scores
array([0.44300752, 0.27772182, 0.3697178 ])
Изменчивость между разбиениями довольно велика! В реальных условиях рекомендуется использовать больше разбиений для лучшей оценки изменчивости. Давайте теперь будем сообщать средние значения CV-оценок и их стандартное отклонение.
print(f"CV MAPE: {cv_mape_scores.mean():.3f} ± {cv_mape_scores.std():.3f}")
CV MAPE: 0.363 ± 0.068
Мы можем вычислить несколько комбинаций метрик оценки и функций потерь, которые немного ниже представлены в отчёте.
from collections import defaultdict
from sklearn.metrics import (
make_scorer,
mean_absolute_error,
mean_pinball_loss,
root_mean_squared_error,
)
from sklearn.model_selection import cross_validate
def consolidate_scores(cv_results, scores, metric):
if metric == "MAPE":
scores[metric].append(f"{value.mean():.2f} ± {value.std():.2f}")
else:
scores[metric].append(f"{value.mean():.1f} ± {value.std():.1f}")
return scores
scoring = {
"MAPE": make_scorer(mean_absolute_percentage_error),
"RMSE": make_scorer(root_mean_squared_error),
"MAE": make_scorer(mean_absolute_error),
"pinball_loss_05": make_scorer(mean_pinball_loss, alpha=0.05),
"pinball_loss_50": make_scorer(mean_pinball_loss, alpha=0.50),
"pinball_loss_95": make_scorer(mean_pinball_loss, alpha=0.95),
}
loss_functions = ["squared_error", "poisson", "absolute_error"]
scores = defaultdict(list)
for loss_func in loss_functions:
model = HistGradientBoostingRegressor(loss=loss_func)
cv_results = cross_validate(
model,
X,
y,
cv=ts_cv,
scoring=scoring,
n_jobs=2,
)
time = cv_results["fit_time"]
scores["loss"].append(loss_func)
scores["fit_time"].append(f"{time.mean():.2f} ± {time.std():.2f} s")
for key, value in cv_results.items():
if key.startswith("test_"):
metric = key.split("test_")[1]
scores = consolidate_scores(cv_results, scores, metric)
Моделирование предсказательной неопределённости через квантильную регрессию#
Вместо моделирования ожидаемого значения распределения \(Y|X\) как это делают метод наименьших квадратов и потерь Пуассона, можно попытаться оценить квантили условного распределения.
\(Y|X=x_i\) ожидается случайной величиной для данной точки данных \(x_i\) потому что мы ожидаем, что количество прокатов не может быть предсказано со 100% точностью по признакам. На это могут влиять другие переменные, не полностью захваченные существующими лаговыми признаками. Например, будет ли дождь в следующий час, нельзя полностью предсказать по данным о прокате велосипедов за прошлые часы. Это то, что мы называем алеаторной неопределённостью.
Квантильная регрессия позволяет дать более детальное описание этого распределения без строгих предположений о его форме.
quantile_list = [0.05, 0.5, 0.95]
for quantile in quantile_list:
model = HistGradientBoostingRegressor(loss="quantile", quantile=quantile)
cv_results = cross_validate(
model,
X,
y,
cv=ts_cv,
scoring=scoring,
n_jobs=2,
)
time = cv_results["fit_time"]
scores["fit_time"].append(f"{time.mean():.2f} ± {time.std():.2f} s")
scores["loss"].append(f"quantile {int(quantile * 100)}")
for key, value in cv_results.items():
if key.startswith("test_"):
metric = key.split("test_")[1]
scores = consolidate_scores(cv_results, scores, metric)
scores_df = pl.DataFrame(scores)
scores_df
Давайте посмотрим на потери, которые минимизируют каждую метрику.
def min_arg(col):
col_split = pl.col(col).str.split(" ")
return pl.arg_sort_by(
col_split.list.get(0).cast(pl.Float64),
col_split.list.get(2).cast(pl.Float64),
).first()
scores_df.select(
pl.col("loss").get(min_arg(col_name)).alias(col_name)
for col_name in scores_df.columns
if col_name != "loss"
)
Даже если распределения оценок перекрываются из-за дисперсии в наборе данных, верно, что средняя RMSE ниже, когда loss="squared_error", тогда как средняя MAPE ниже, когда loss="absolute_error" как ожидалось. Это также верно для средней пинбол-потери с квантилями 5 и 95. Оценка, соответствующая потере для квантиля 50, перекрывается с оценкой, полученной минимизацией других функций потерь, что также верно для MAE.
Качественный взгляд на предсказания#
Теперь мы можем визуализировать производительность модели относительно 5-го процентиля, медианы и 95-го процентиля:
all_splits = list(ts_cv.split(X, y))
train_idx, test_idx = all_splits[0]
X_train, X_test = X[train_idx, :], X[test_idx, :]
y_train, y_test = y[train_idx], y[test_idx]
max_iter = 50
gbrt_mean_poisson = HistGradientBoostingRegressor(loss="poisson", max_iter=max_iter)
gbrt_mean_poisson.fit(X_train, y_train)
mean_predictions = gbrt_mean_poisson.predict(X_test)
gbrt_median = HistGradientBoostingRegressor(
loss="quantile", quantile=0.5, max_iter=max_iter
)
gbrt_median.fit(X_train, y_train)
median_predictions = gbrt_median.predict(X_test)
gbrt_percentile_5 = HistGradientBoostingRegressor(
loss="quantile", quantile=0.05, max_iter=max_iter
)
gbrt_percentile_5.fit(X_train, y_train)
percentile_5_predictions = gbrt_percentile_5.predict(X_test)
gbrt_percentile_95 = HistGradientBoostingRegressor(
loss="quantile", quantile=0.95, max_iter=max_iter
)
gbrt_percentile_95.fit(X_train, y_train)
percentile_95_predictions = gbrt_percentile_95.predict(X_test)
Теперь мы можем взглянуть на предсказания, сделанные регрессионными моделями:
last_hours = slice(-96, None)
fig, ax = plt.subplots(figsize=(15, 7))
plt.title("Predictions by regression models")
ax.plot(
y_test[last_hours],
"x-",
alpha=0.2,
label="Actual demand",
color="black",
)
ax.plot(
median_predictions[last_hours],
"^-",
label="GBRT median",
)
ax.plot(
mean_predictions[last_hours],
"x-",
label="GBRT mean (Poisson)",
)
ax.fill_between(
np.arange(96),
percentile_5_predictions[last_hours],
percentile_95_predictions[last_hours],
alpha=0.3,
label="GBRT 90% interval",
)
_ = ax.legend()
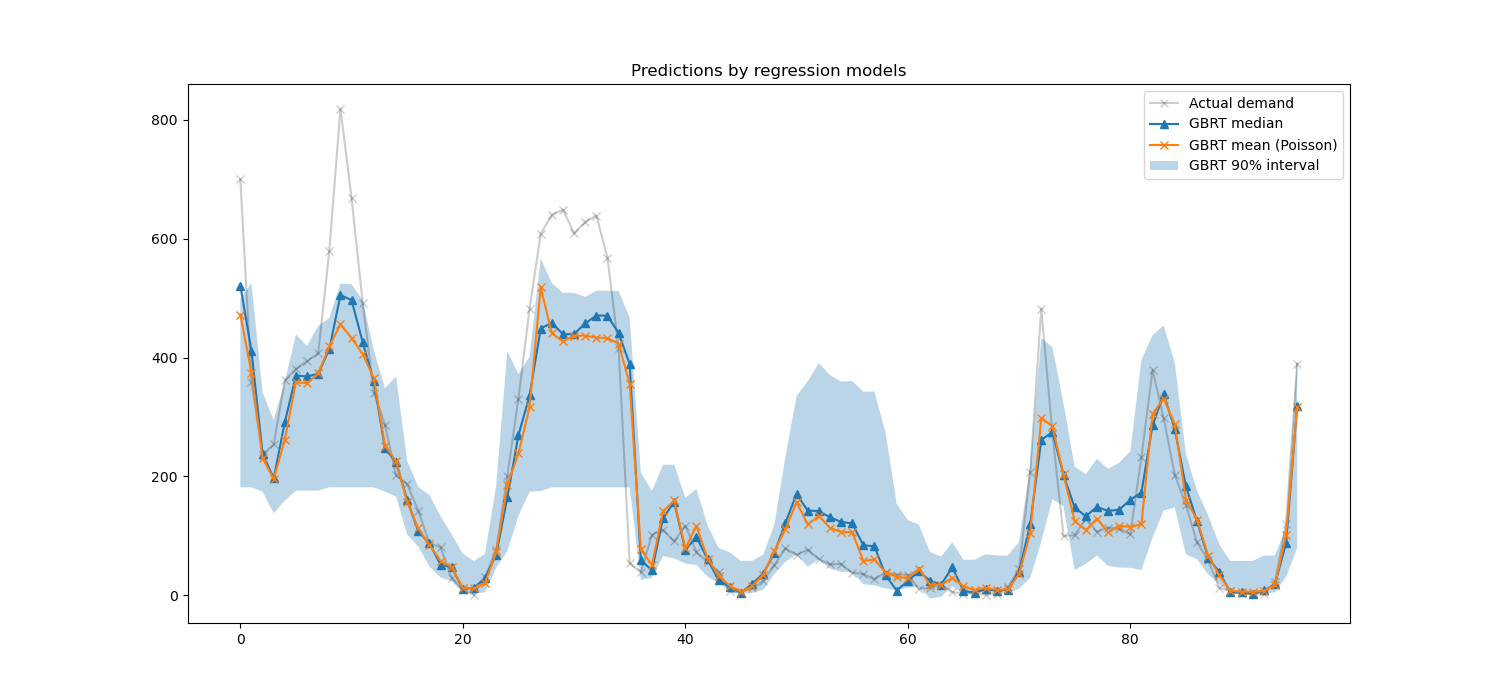
Здесь интересно заметить, что синяя область между 5% и 95% процентильными оценщиками имеет ширину, которая варьируется в зависимости от времени суток:
Ночью синяя полоса намного уже: пара моделей довольно уверена, что будет небольшое количество прокатов велосипедов. И более того, это кажется правильным в том смысле, что фактический спрос остаётся в этой синей полосе.
В течение дня синяя полоса намного шире: неопределенность растет, вероятно, из-за изменчивости погоды, которая может иметь очень большое влияние, особенно в выходные дни.
Мы также можем видеть, что в будние дни паттерн поездок на работу все еще виден в оценках 5% и 95%.
Наконец, ожидается, что в 10% случаев фактический спрос не лежит между 5% и 95% перцентильными оценками. На этом тестовом промежутке фактический спрос кажется выше, особенно в часы пик. Это может указывать, что наш 95% перцентильный оценщик недооценивает пики спроса. Это можно количественно подтвердить, вычислив эмпирические показатели покрытия, как сделано в калибровка доверительных интервалов.
Рассматривая производительность нелинейных регрессионных моделей по сравнению с лучшими моделями:
from sklearn.metrics import PredictionErrorDisplay
fig, axes = plt.subplots(ncols=3, figsize=(15, 6), sharey=True)
fig.suptitle("Non-linear regression models")
predictions = [
median_predictions,
percentile_5_predictions,
percentile_95_predictions,
]
labels = [
"Median",
"5th percentile",
"95th percentile",
]
for ax, pred, label in zip(axes, predictions, labels):
PredictionErrorDisplay.from_predictions(
y_true=y_test,
y_pred=pred,
kind="residual_vs_predicted",
scatter_kwargs={"alpha": 0.3},
ax=ax,
)
ax.set(xlabel="Predicted demand", ylabel="True demand")
ax.legend(["Best model", label])
plt.show()
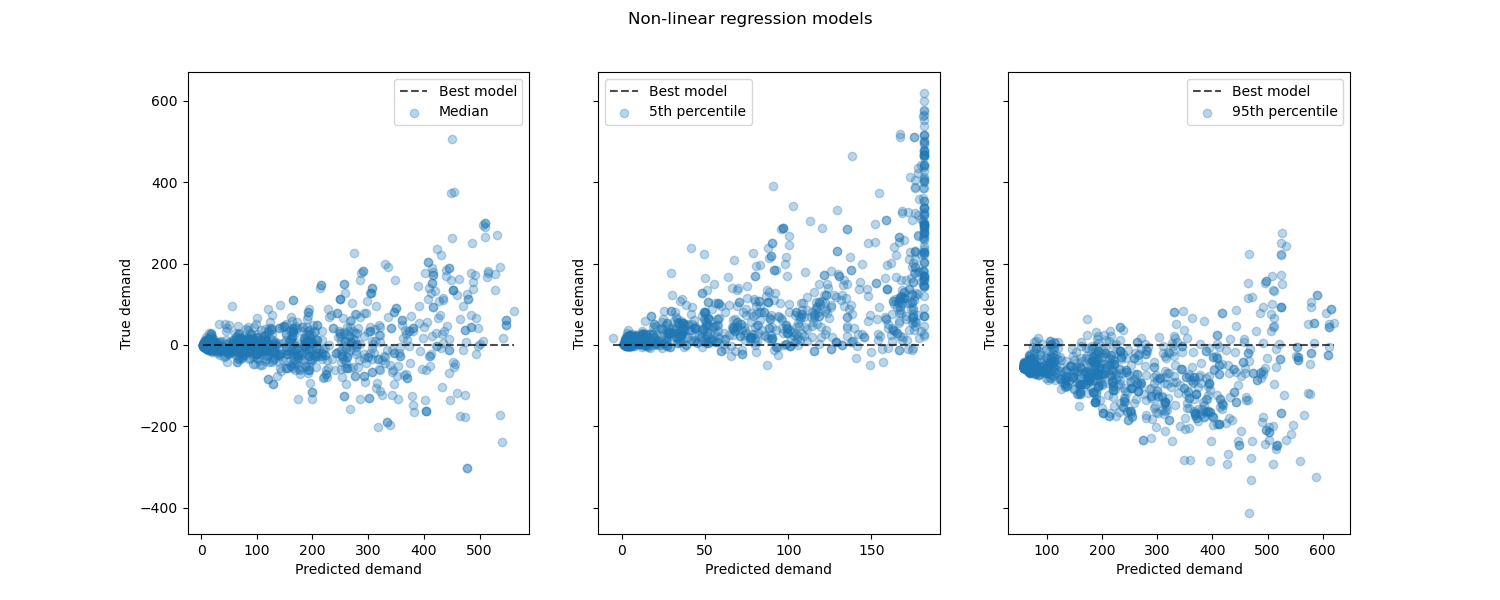
Заключение#
В этом примере мы исследовали прогнозирование временных рядов с использованием лаговых
признаков. Мы сравнили наивную регрессию (используя стандартизированный
train_test_split) с правильной
стратегией оценки временных рядов с использованием
TimeSeriesSplit. Мы заметили, что модель, обученная с использованием train_test_split, имеющий значение по умолчанию shuffle установлено в True дал слишком
оптимистичную среднюю абсолютную процентную ошибку (MAPE). Результаты,
полученные при временном разделении, лучше отражают производительность
нашей модели регрессии временных рядов. Мы также проанализировали прогностическую неопределенность
нашей модели с помощью квантильной регрессии. Предсказания на основе 5-го и
95-го процентилей с использованием loss="quantile" предоставить нам количественную оценку
неопределенности прогнозов, сделанных нашей моделью регрессии временных рядов.
Оценка неопределенности также может быть выполнена
с использованием MAPIE,
которая предоставляет реализацию на основе последних работ по методам конформного предсказания
и оценивает одновременно как алеаторическую, так и эпистемическую неопределенность.
Кроме того, функциональность, предоставляемая sktime
может использоваться для расширения оценщиков scikit-learn с помощью рекурсивного прогнозирования временных рядов, что позволяет динамически предсказывать будущие значения.
Общее время выполнения скрипта: (0 минут 10.730 секунд)
Связанные примеры
Баланс сложности модели и кросс-валидационной оценки

Интервалы прогнозирования для регрессии градиентного бустинга
Признаки в деревьях с градиентным бустингом на гистограммах
