Примечание

Перейти в конец чтобы скачать полный пример кода или запустить этот пример в браузере через JupyterLite или Binder.

Дискретизация признаков#

Демонстрация дискретизации признаков на синтетических классификационных наборах данных. Дискретизация признаков разлагает каждый признак на набор бинов, здесь равномерно распределенных по ширине. Дискретные значения затем кодируются методом one-hot и передаются линейному классификатору. Такая предобработка позволяет получить нелинейное поведение, даже несмотря на то, что классификатор является линейным.

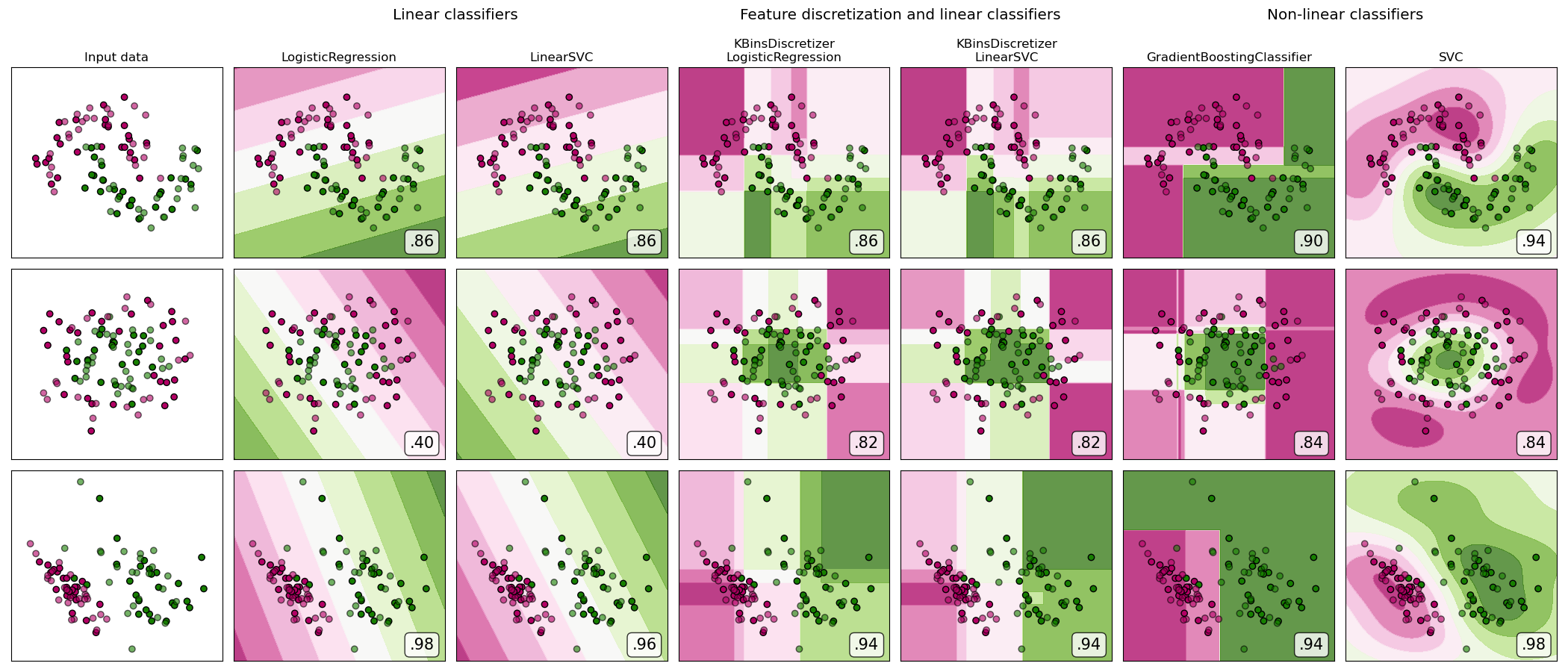
В этом примере первые две строки представляют линейно неразделимые наборы данных (луны и концентрические круги), а третья приблизительно линейно разделима. На двух линейно неразделимых наборах данных дискретизация признаков значительно повышает производительность линейных классификаторов. На линейно разделимом наборе данных дискретизация признаков снижает производительность линейных классификаторов. Для сравнения также показаны два нелинейных классификатора.

Этот пример следует воспринимать с долей скептицизма, так как передаваемая интуиция не обязательно переносится на реальные наборы данных. Особенно в высокоразмерных пространствах данные могут легче разделяться линейно. Более того, использование дискретизации признаков и one-hot кодирования увеличивает количество признаков, что легко приводит к переобучению при малом количестве образцов.

На графиках показаны обучающие точки сплошными цветами и тестовые точки полупрозрачными. В правом нижнем углу показана точность классификации на тестовом наборе.

Input data, LogisticRegression, LinearSVC, KBinsDiscretizer LogisticRegression, KBinsDiscretizer LinearSVC, GradientBoostingClassifier, SVC

dataset 0
---------
LogisticRegression: 0.86
LinearSVC: 0.86
KBinsDiscretizer + LogisticRegression: 0.86
KBinsDiscretizer + LinearSVC: 0.86
GradientBoostingClassifier: 0.90
SVC: 0.94

dataset 1
---------
LogisticRegression: 0.40
LinearSVC: 0.40
KBinsDiscretizer + LogisticRegression: 0.82
KBinsDiscretizer + LinearSVC: 0.82
GradientBoostingClassifier: 0.84
SVC: 0.84

dataset 2
---------
LogisticRegression: 0.98
LinearSVC: 0.96
KBinsDiscretizer + LogisticRegression: 0.94
KBinsDiscretizer + LinearSVC: 0.94
GradientBoostingClassifier: 0.94
SVC: 0.98

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

import matplotlib.pyplot as plt
import numpy as np
from matplotlib.colors import ListedColormap

from sklearn.datasets import make_circles, make_classification, make_moons
from sklearn.ensemble import GradientBoostingClassifier
from sklearn.exceptions import ConvergenceWarning
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import GridSearchCV, train_test_split
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import KBinsDiscretizer, StandardScaler
from sklearn.svm import SVC, LinearSVC
from sklearn.utils._testing import ignore_warnings

h = 0.02  # step size in the mesh


def get_name(estimator):
    name = estimator.__class__.__name__
    if name == "Pipeline":
        name = [get_name(est[1]) for est in estimator.steps]
        name = " + ".join(name)
    return name


# list of (estimator, param_grid), where param_grid is used in GridSearchCV
# The parameter spaces in this example are limited to a narrow band to reduce
# its runtime. In a real use case, a broader search space for the algorithms
# should be used.
classifiers = [
    (
        make_pipeline(StandardScaler(), LogisticRegression(random_state=0)),
        {"logisticregression__C": np.logspace(-1, 1, 3)},
    ),
    (
        make_pipeline(StandardScaler(), LinearSVC(random_state=0)),
        {"linearsvc__C": np.logspace(-1, 1, 3)},
    ),
    (
        make_pipeline(
            StandardScaler(),
            KBinsDiscretizer(
                encode="onehot", quantile_method="averaged_inverted_cdf", random_state=0
            ),
            LogisticRegression(random_state=0),
        ),
        {
            "kbinsdiscretizer__n_bins": np.arange(5, 8),
            "logisticregression__C": np.logspace(-1, 1, 3),
        },
    ),
    (
        make_pipeline(
            StandardScaler(),
            KBinsDiscretizer(
                encode="onehot", quantile_method="averaged_inverted_cdf", random_state=0
            ),
            LinearSVC(random_state=0),
        ),
        {
            "kbinsdiscretizer__n_bins": np.arange(5, 8),
            "linearsvc__C": np.logspace(-1, 1, 3),
        },
    ),
    (
        make_pipeline(
            StandardScaler(), GradientBoostingClassifier(n_estimators=5, random_state=0)
        ),
        {"gradientboostingclassifier__learning_rate": np.logspace(-2, 0, 5)},
    ),
    (
        make_pipeline(StandardScaler(), SVC(random_state=0)),
        {"svc__C": np.logspace(-1, 1, 3)},
    ),
]

names = [get_name(e).replace("StandardScaler + ", "") for e, _ in classifiers]

n_samples = 100
datasets = [
    make_moons(n_samples=n_samples, noise=0.2, random_state=0),
    make_circles(n_samples=n_samples, noise=0.2, factor=0.5, random_state=1),
    make_classification(
        n_samples=n_samples,
        n_features=2,
        n_redundant=0,
        n_informative=2,
        random_state=2,
        n_clusters_per_class=1,
    ),
]

fig, axes = plt.subplots(
    nrows=len(datasets), ncols=len(classifiers) + 1, figsize=(21, 9)
)

cm_piyg = plt.cm.PiYG
cm_bright = ListedColormap(["#b30065", "#178000"])

# iterate over datasets
for ds_cnt, (X, y) in enumerate(datasets):
    print(f"\ndataset {ds_cnt}\n---------")

    # split into training and test part
    X_train, X_test, y_train, y_test = train_test_split(
        X, y, test_size=0.5, random_state=42
    )

    # create the grid for background colors
    x_min, x_max = X[:, 0].min() - 0.5, X[:, 0].max() + 0.5
    y_min, y_max = X[:, 1].min() - 0.5, X[:, 1].max() + 0.5
    xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))

    # plot the dataset first
    ax = axes[ds_cnt, 0]
    if ds_cnt == 0:
        ax.set_title("Input data")
    # plot the training points
    ax.scatter(X_train[:, 0], X_train[:, 1], c=y_train, cmap=cm_bright, edgecolors="k")
    # and testing points
    ax.scatter(
        X_test[:, 0], X_test[:, 1], c=y_test, cmap=cm_bright, alpha=0.6, edgecolors="k"
    )
    ax.set_xlim(xx.min(), xx.max())
    ax.set_ylim(yy.min(), yy.max())
    ax.set_xticks(())
    ax.set_yticks(())

    # iterate over classifiers
    for est_idx, (name, (estimator, param_grid)) in enumerate(zip(names, classifiers)):
        ax = axes[ds_cnt, est_idx + 1]

        clf = GridSearchCV(estimator=estimator, param_grid=param_grid)
        with ignore_warnings(category=ConvergenceWarning):
            clf.fit(X_train, y_train)
        score = clf.score(X_test, y_test)
        print(f"{name}: {score:.2f}")

        # plot the decision boundary. For that, we will assign a color to each
        # point in the mesh [x_min, x_max]*[y_min, y_max].
        if hasattr(clf, "decision_function"):
            Z = clf.decision_function(np.column_stack([xx.ravel(), yy.ravel()]))
        else:
            Z = clf.predict_proba(np.column_stack([xx.ravel(), yy.ravel()]))[:, 1]

        # put the result into a color plot
        Z = Z.reshape(xx.shape)
        ax.contourf(xx, yy, Z, cmap=cm_piyg, alpha=0.8)

        # plot the training points
        ax.scatter(
            X_train[:, 0], X_train[:, 1], c=y_train, cmap=cm_bright, edgecolors="k"
        )
        # and testing points
        ax.scatter(
            X_test[:, 0],
            X_test[:, 1],
            c=y_test,
            cmap=cm_bright,
            edgecolors="k",
            alpha=0.6,
        )
        ax.set_xlim(xx.min(), xx.max())
        ax.set_ylim(yy.min(), yy.max())
        ax.set_xticks(())
        ax.set_yticks(())

        if ds_cnt == 0:
            ax.set_title(name.replace(" + ", "\n"))
        ax.text(
            0.95,
            0.06,
            (f"{score:.2f}").lstrip("0"),
            size=15,
            bbox=dict(boxstyle="round", alpha=0.8, facecolor="white"),
            transform=ax.transAxes,
            horizontalalignment="right",
        )


plt.tight_layout()

# Add suptitles above the figure
plt.subplots_adjust(top=0.90)
suptitles = [
    "Linear classifiers",
    "Feature discretization and linear classifiers",
    "Non-linear classifiers",
]
for i, suptitle in zip([1, 3, 5], suptitles):
    ax = axes[0, i]
    ax.text(
        1.05,
        1.25,
        suptitle,
        transform=ax.transAxes,
        horizontalalignment="center",
        size="x-large",
    )
plt.show()